Throughout my conversations about Fund I/O over the past couple of weeks, one thing has become clear: Fund I/O implies a radically different way of thinking about business.

What is the Fund I/O business model? Fund I/O is a business model for the production of goods with substantial economies of scale. In a nutshell:

• Financing is provided through presales made during a crowdfunding campaign.
• The producer commits in advance to a pricing scheme that passes savings due to economies of scale on to customers directly, by lowering prices as fast as possible.
• Early buyers are guaranteed to get a refund when the price drops, so that they have no incentive to wait with their purchase.

If you are looking for details, good places to start are fund-io.com and this example.

What makes Fund I/O different from the conventional way of doing business? Suppose you run a company and want to produce a product that benefits from economies of scale. Here is what Fund I/O means to you:

• You finance your product entirely through presales. You do not have take on a loan, you do not have to pay interest, and you do not have to maximize profit for your investors. This drastically reduces your risk and your cost of capital. The presales appear as a non-interest bearing liability on your balance sheet, and the primary interest of your financiers is to receive a great product, not to get paid.
• You place an absolute limit on the profit you can make off a product. This limit can be chosen arbitrarily, but by choosing a refund scheme you are committing to an absolute limit on your profits. Note that because you used presales from customers to finance production you are making a profit without having invested any capital yourself, so from that point of view your return on investment is infinite, even if your maximum profits are not!
• You obtain a tremendous amount of market information: By committing to a refund scheme, you give your customers an incentive to reveal exactly how much they are willing to pay for your product. This translates into higher sales, more revenue and faster growth.

Through the combination of crowdfunding, a clear price reduction scheme with a limit on profits and a refund mechanism, Fund I/O manages to align the interests of key stakeholders and it provides them with a mechnism to communicate truthfully about value: It resolves the fundamental conflict of interest between investors who want to maximize their profits and customers who want to minimize what they have to pay.

What makes Fund I/O different from other crowdfunding schemes? There are basically two different crowdfunding models out there: reward-based crowdfunding and equity crowdfunding.

Equity crowdfunding is not that different from the conventional business model. Financiers are still interested in return on investment. The key difference is that investors often have another stake in the business in addition to their profit interests. For example, they may be not only investors but customers at the same time, or they may have an interest in the social impact of the business. But still the business is obliged to maximize profits on behalf of its investors, which gives customers incentives to understate their valuation of the products the business is offering.

Reward-based crowdfunding makes customers the financiers of a product, aligning the interests of two key stakeholders. But it still does not provide a mechanism to communicate about value. In reward-based crowdfunding, creators have to fix the price a priori and often a majority of backers pledge just this price and no more. The success of reward-based crowdfunding hinges on the generosity of backers who self-select for price targeting by willingly paying a large premium for the product. This type of altruism (whether motivated by appreciation of the project, the thrill of being part of something great or the enjoyment of receiving secondary merchandise) is great, if it suffices to finance the project. Fund I/O can be tweaked to captialize on this type of gift economy as well, but the main contribution of Fund I/O lies elsewhere: Fund I/O makes crowdfunding work in cases where the capital requirements of a project are large or where the potential customers are price sensitive. Fund I/O provides the mechanism that allows producers and customers to join forces in order to create great products, even if all parties involved need to avoid paying more than they have to.

What problem does Fund I/O solve? From the point of view of a business, Fund I/O reduces risk, aligns interests of stakeholders, provides a wealth of market information and generates more sales. Moreover Fund I/O provides financing alternatives to debt and equity and conventional crowdfunding. This is particularly useful in cases where debt and equity are too expensive, too risky or simply unavailable and when altruistic contributions made through a rewards-based crowdfunding campaign do not suffice.

However, this is just one angle on the question: “What problem does Fund I/O solve?” Over the next days, I will post other answers, taking the point of view of a customer, or examining the applicability of Fund I/O to non-profit projects aimed at social impact. One very technical answer is already written up: Fund I/O provides a practical implementation of an incentive compatible, individually rational mechanism for the private provision of excludable public goods that is asymptotically optimal.

Fair crowdfunding has a new home: Fund I/O.

As you may have seen, I have been blogging recently about a new crowdfunding mechanism for public goods, the Average Cost Threshold Protocol. Since the last post on the topic, I have spent quite some time discussing this idea with people, and have decided to give this idea into a project dubbed Fund I/O with an own website fund-io.com and an own Twitter account.

To get updates about his project and idea, you can subscribe to a (very-low volume) mailing list on the project website, or just follow this blog. I’ll keep posting whatever I have to say on the subject of fair crowdfunding on this blog. (If and when Fund I/O gets its own blog, I will make an announcement here.)

Finally, in case you are wondering, Fund I/O is not a startup. (Not yet, anyway.) The current goal of Fund I/O is to try some variant of the ACTP in practice. If you have got just the right project in need of a revolutionary funding mechansim, let me know!

There are many beautiful geometric interpretations of the GCD and visualizations of the Euclidean algorithm out there, see for example here, here and here. I have written about this myself some time ago. But I find that some of the pictures become much clearer when lifted into the third dimension.

[Note: I am using Sage Cells to produce the pictures in this post. This has the advantage that you, dear reader, can interact with the pictures by modifying the Sage code. However, this will probably not run everywhere. It certainly won’t work in most RSS readers…]

Here is the graph of the GCD! First a little static preview…

… and now a proper interactive graph. Be sure to rotate the image to get a 3d impression. (Requires Java…)

What precisely are we seeing here? The gcd is a function $\mathrm{gcd}:\mathbb{N}^2\rightarrow\mathbb{N}$. Its graph is a (countable) set of points in $\mathbb{N}^3$. This graph is precisely the set of integer points contained in one of the (countably many) lines indicated in the above picture. The value of the gcd is given by the vertical axis.

Now, what are those lines? Suppose $a$ and $b$ are two natural numbers that are relatively prime, i.e., $\gcd(a,b)=1$. Then we know that $\gcd(ka,kb)=k$ for any positive integer $k$. So all (positive) integer points on the line through the origin and $(a,b,1)$ are in the graph of the gcd. Conversely, for any numbers $x,y$ with $gcd(x,y)=z$, we know that $\gcd(\frac{x}{z},\frac{y}{z})=1$, that is, the point $(x,y,z)$ lies on the line through the origin and $(\frac{x}{z},\frac{y}{z},1)$. So by drawing all these lines, we can be sure we hit all the integer points in the graph of the gcd.

What I find very beautiful about this is that when looking at this picture from the right angle, you can see the binary tree structure of this set of lines. It is precisely this binary tree that we walk along when running the Euclidean algorithm. The lines in the above picture are color coded by their depth in this “Euclidean” binary tree.

The version of the Euclidean algorithm I like best this one. Suppose you want to find $\gcd(a,b)=1$. If $a>b$, compute $\gcd(a-b,b)$. If $a<b$, compute $\gcd(a,b-a)$. If $a=b$, we are done and the number $a=b$ is the gcd. At each point in the algorithm we make a choice, depending on whether $a>b$ or $a<b$. If we keep track of these choices by writing down a 1 in the former case and a 0 in the latter, then, for any pair (a,b), we get a word of 0s and 1s that describes a path through a binary tree. As we walk from one pair $(a,b)$ to the next in this fashion, we trace out a path in the plane: For each 1 we take a horizontal step and for each 0 we take a vertical step. This path can look as follows.

Now comes the twist. We can turn the Euclidean algorithm upside down. Instead of walking from the point $(a,b)$ to a point of the form $(g,g)$ and thus finding the gcd, we can also start from the point $(1,1)$ and walk to a point of the form $(\frac{a}{g},\frac{b}{g})$ to find the gcd $g$. (Why $(\frac{a}{g},\frac{b}{g})$? Well, $(\frac{a}{g},\frac{b}{g})$ is the primitive lattice vector in the direction of $(a,b)$. In terms of the graph at the top, $(\frac{a}{g},\frac{b}{g},1)$ is the starting point of the ray through $(a,b,\gcd(a,b))$.)

How do we get there? We start out by fixing the lattice basis with “left” basis vector $(0,1)$ and “right” basis vector $(1,0)$. Their sum $(1,1)$, which I call the “center”, is a primitive lattice vector. Now we ask ourselves: is the point $(a,b)$ to the left or to the right of the line through the center? If it is to the left of that line, we continue with the basis $(0,1)$ and $(1,1)$. If it is to the right of that line, we continue with the basis $(1,1)$ and $(1,0)$ and recurse: We take the sum of our two new basis vectors as the new center and ask if $(a,b)$ lies to the left or to the right of the line through the center, and continue accordingly. If $(a,b)$ lies on the line through the center, we are done: the gcd of $a$ and $b$ is the factor by which I have to multiply the center to get to $(a,b)$.

As we follow this algorithm, we draw the path from one center to the next, until we reach $(\frac{a}{g},\frac{b}{g})$. Then we get the following picture. It looks almost like a straight line from $(1,1)$ to our goal, but it is only straight whenever we take two consecutive left turns or two consecutive right turns. Whenever we alternate between right and left, we have a proper angle, it only gets difficult to see this angle the farther out we get. If we write down a sequence of 1s and 0s, corresponding to the left and right turns we take, we get the exact same sequence as with the standard Euclidean algorithm.

The obvious next step is to draw the complete binary trees given by the above two visualizations of the Euclidean algorithm (up to a certain maximum depth). Drawing the first tree gives a big mess, because many of the edges of the tree overlap. You can clean up the picture by removing the lines and drawing only the points: In the code below comment the first definition of thisdrawing and uncomment the second. This then gives you a picture of all primitive lattice points (pairs of relatively prime numbers) in the plane at depth at most maxdepth in the tree.

The second variant of the Euclidean algorithm gives a much nicer picture, revealing the fractal nature of the set of primitive lattice points. The nodes of the tree, i.e., the points drawn in the picture are the starting points of the rays plotted in the 3d graph of the gcd given at the beginning of this post. In this way, this drawing of the tree gives the precise structure of the binary tree intuitively visible in the three-dimensional graph. One thing you may want to try is to increase the maxdepth of the tree to 10. (Warning: this may take much longer to render!) Note how far out from the origin some of the points at depths 10 are.

The reader may have observed that the binary tree described in this post gives us a very nice way of enumerating the rational numbers. Calkin and Wilf made this observation in the paper Recounting the Rationals, whence it is sometimes called the Calkin-Wilf tree, even though Euclid tree might be a better name as it is given by the Euclidean algorithm itself. As we have seen above, a look through the lens of lattice geometry tells us how to draw this tree in the plane and how to find it in the graph of the GCD.

Can fair crowdfunding resolve the conflict over copyright? Or, as Cory Doctorow put it yesterday:

Does the Average Cost Threshold Protocol incentivize content creators to “sue the Internet”?

Very short answer: The incentive for creators to sue the Internet is very small (much smaller than usual) but not zero.

Short answer: The Average Cost Threshold Protocol (ACTP) drastically reduces the incentive of content creators to sue people, as creators’ costs are covered from the start. Moreover it drastically reduces the incentive for people to copy content outside of what is allowed by the protocol, because buyer’s payments are used to lower the price (for themselves and others) and to eventually release the content under a copyleft license.

That said, there is a “sales phase” in the protocol where such incentives exist, even if they are limited. However, this drawback is outweighed by the protocol’s key advantages:

• Creators can expect to raise significantly more money than with funding models that employ only copyleft licenses.
• Creators and users agree from the outset on a clear path towards release of the content under a copyleft license.

Moreover the protocol can be modified so that creators have no incentive whatsoever to sue the Internet - however, in this case creators also lack an economic incentive to deliver a great product.

Long answer: Here are the key reasons why creators have very little incentive to sue the internet, if they choose to adopt the ACTP.

• The protocol guarantees that creators’ costs are covered before content is ever released. This drastically reduces the creators’ financial risk, which in turn reduces the threat unlicensed copies pose to creators.
• Costs are covered by users, not investors. This frees creators from having to worry about paying back loans or maximizing their return on equity. Thus the creators’ economic goal is to maximize user value not shareholder value.
• The ACTP provides a clear path towards releasing the content under a copyleft license. By adopting the ACTP, creators subscribe willingly to this goal.
• Creators’ profits are maximized if and only if the content is released under a copyleft license, at the end of ACTP. This means that creators’ have an incentive to work towards the goal of releasing the content for free.

That being said, the ACTP does have a “sales phase” where the content is available only under a “closed” copyright license and people have to buy access. In this sales phase, users have an economic incentive to obtain unlicensed copies.

• Creators receive a share of the revenues earned during the sales phase as profit. They thus have an incentive to sue people who avoid paying for access in the sales phase.
• However, if there are enough buyers to “free” the content and cause its release under a copyleft license, then the creators do not care how many people made unlicensed copied during the sales phase: their profits in this case are fixed from the start.
• The ACTP could be modified so that creators do not receive any profits during the sales phase. All revenues from sales could go towards lowering the price by refunding previous buyers/backers. In this case creators do not have any incentive whatsoever to sue the Internet, at any point in time. However, I do not think that this is a good idea. Because in this case, creators’ do not receive any revenue after the initial fundraising campaign and thus they have no economic incentive to make their product shine and promote it accordingly.

Moreover, the ACTP provides incentives for users to actively participate in the sales phase of the protocol by paying, instead of by making or obtaining unlicensed copies:

• In the short term, the more people pay, the faster the price will drop. As a buyer this means you yourself will get a larger refund and at the same time you will enable other people to afford access.
• In the long run, the more people pay, the sooner will the content be released freely, under a copyleft license.

The sales phase thus becomes a cooperative game among users, where they can help each other by lowering the price in the short term and ultimately “freeing” the content for everyone. This of course has the drawback that it might cause cooperative users (who buy) to sue uncooperative users (who make or obtain unlicensed copies). But the amount of refund money cooperative users stand to loose from unlicensed copies is very limited, so I hope this is not going to be an issue. Users who obtain unlicensed copies hurt themselves by making it less likely that the content is eventually going to be officially released under a copyleft license.

But why should we have a “sales phase” at all? Would it not be better to release the content under a copyleft license right away? The reason is a phenomenon that has been well-studied in the economics literature: By restricting access to content during the sales phase, it is possible to raise significantly larger amounts of funds for the creation of digital content than would otherwise be possible. In economics jargon: It is significantly easier to raise funds for the private provision of a public good with use exclusions than for the private provision of a pure public good without use exclusions. The amount of money we can raise for content that is going to published under a copyleft license from the start grows on the order of $\sqrt{n}$ where $n$ is the number of people in the economy. If we introduce use exclusions, on the other hand, the amount of money grows on the order of $n$. This is a difference of several orders of magnitude, with a huge potential impact in practice! (I will write more about these results in a future post. In the meantime I recommend this post and these two articles.) The ACTP aims to strike a balance between the conflicting goals of publishing free content and raising funds by employing use exclusions in an intermediate phase and providing a clear path towards release under a copyleft license.

Bottom-line: The ACTP does a far better job of aligning incentives than any other mechanism for funding digital content that I know. I think it goes a long way towards resolving the economic conflict over copyright and I can’t wait to put it into practice and try it out.

We live in a wonderful age! So much that we value - music, movies, books, games, software, designs, research, art, ideas - can be stored in digital form. Once these digital goods are created, they could in principle be made available to everyone at virtually no extra cost. So why don’t we? Why do we fight about copyright instead?

The reason is a conflict of economic interests. On the one hand we need to fund the creation of digital goods. On the other hand, our creation can do the most good if it is made available to literally everyone. But how can we convince people to pay for a digital good, if they know that eventually everybody can download a copy for free? What we need is a new idea that addresses both of these issues: the public welfare and the profitability of creating digital goods.

In this regard crowdfunding platforms are very promising, as they can in principle be used to fund digital goods that are then made freely available to everybody. However, a closer look reveals that in practice the digital goods financed by crowdfunding campaigns are often sold like apples - as if they could not be copied at all. Here is one idea how we can do better:

The Average Cost Threshold Protocol is a fair crowdfunding mechanism that takes economic interests of both users and creators into account.

How it works is best explained by way of a concrete example. Suppose a company wants to raise \$1,000,000 to finance the production of a computer game. They start a crowdfunding campaign on a website implementing the Average Cost Threshold Protocol. The website starts collecting pledges until a deadline is reached. Suppose on the day of the deadline the pledge look as in picture below. In particular, we find that there are 20,000 people who pledged \$50 each or more. If all of them pay exactly \$50, then the company’s costs will be covered and everybody will have paid the same amount. Moreover \$50 is the lowest price that covers costs: for example 24,000 people would be willing to pay \$40, but that yields only \$960,000. This lowest price now becomes the threshold price: everybody who pledged at least \$50 pays exactly \$50 and they become backers, who will receive a copy of the game once it is finished. All others do not pay anything and do not get a copy. The principle is simple: the costs of production are distributed equally among all those who get access. The threshold price is chosen such that it provides access to the largest number of people at the lowest possible price such that the costs of production are covered.

Now that the game is released, more people have heard about it and want to purchase access. Typically, the company would simply sell copies and keep the revenues as profit. But here comes the twist! Instead of paying a fixed price, interested buyers submit pledges on what they would be willing to pay for the game. Suppose there are another 10,000 people who each pledge \$40 or more. Then we drop the price to \$40 dollars and charge each newcomer \$40 for a copy of the game. The revenues of \$400,000 are split 50-50. One half goes as profit to the company. The other half goes to the original backers, who each get a refund of \$10. Following this principle the price keeps dropping the more people buy the game and thanks to the refunds everybody who gets access is guaranteed to pay the same price no matter how much they pledge or when they pledge.

The more people buy the game, the lower the price for everyone. And the lower the price, the more people can afford to buy the game! What if this virtuous cycle takes off and the game becomes really popular? At this point another feature of the mechanism kicks in: At the very beginning of the crowdfunding campaign a price of freedom of \$10 is announced. This means that as soon as the threshold price drops to the price of freedom of \$10, the game is made available to everyone, the whole world, no matter if they paid or not. This includes the release of the game under a copyleft license as well as the publication of all source code and assets, to allow people to freely modify the game. In the example, the price of freedom of \$10 is reached if the game becomes so popular that at least 180,000 people buy the game. In this scenario, the company has not only covered its costs, but on top of that it also made a profit of \$800,000. (This amounts to an infinite (!) return on investment as the customers contributed all the funding for the project!) The public gains a game they are free to use and modify. And the backers and buyers of the project spent only \$10 each, both to gain early access to the game and to make all of this happen.

We can even go one step further and allow every customer to set their own price of freedom, that is, the price below which they do not care to receive refunds. With this small modification, it is entirely rational for people to pledge exactly as much as they are really willing to pay for the game. This is a truly amazing property that most other methods of raising funds do not satisfy. In a retail sales context, on Kickstarter, in you-name-your-price mechanisms like the Humble Bundle, customers always have an incentive to understate how much the product is worth to them. Here, even entirely self-interested customers have an incentive to tell the truth, at every point during the process. This is not the end of the story, though! The Average Cost Threshold Protocol has a host of variations and wonderful theoretical properties.

As you can see, there is a lot of room to improve upon existing methods for funding digital goods. In a world where digital goods make up an ever increasing percentage of the global economic output this can have a profound impact on our economic lives. With new ideas and experiments we can come up with business models that can raise large amounts of money to finance the creation of high-quality digital goods and at the same time make sure that as many people as possible get access. In particular, we can provide a clear path towards releasing digital goods under a copyleft license. This way, everybody can benefit from the economic power of copying!

Christopher Smy asked for a geometric proof of the identity $$1^3+\ldots+n^3 = (1+\ldots+n)^2.$$ Because I like that sort of thing, I couldn’t resist drawing a picture:

If you like that sort of thing, check out this video or these lecture notes.

A while ago, I started a series of posts on finding new ways to fund public goods. Crowd-funding platforms, which have been enormously successful in 2012, promise a new way of financing creative projects and many of them employ the Street Performer Protocol, which was originally invented with a view towards financing public goods such as open source software projects. However, a closer look at the way the Street Performer Protocol is used on Kickstarter reveals that it is rarely employed to finance goods published under a copyleft license. Rather pledges are treated as pre-orders for goods sold as if they were classic private goods. I think we can do better than that!

In this post, I want to describe a different way to fund the private provision of public goods: the Average Cost Threshold Protocol.

Before we get started, let me clarify what I mean by the term public good. The term does not have the egalitarian meaning of a common good that is shared by everyone and that all members of a community are entitled to. Rather, a public good is any good that has a specific economic property: If a public good is provided to one person, it could also be provided to everybody else at no additional cost. Note that I am not saying the public good actually is provided to everyone. It may very well be that some people are excluded from using the public good. Also, I am not saying that nobody has to pay anything for the public good.

Practically all digital goods are natural public goods. This includes movies, music, ebooks, online lectures, scientific articles, software and computer games. These can, in principle, be copied at virtually no cost. Often, legal or technical restrictions are placed on copying these goods, as producers want to raise money for the provision of these goods by selling these goods as private goods (or by selling advertising tied to these goods). This post is about finding better ways to fund the creation of such digital goods. As my running example of a public good, I am going to use a computer game. Not because games are the most important type of public good, but simply because they are widely popular, require no maintenance after their release (or after, say, the tenth patch) and because a number of computer games have been very successful on Kickstarter, which shows that the audience is open to experimenting with new funding mechanisms.

The Theory of Average Cost Pricing of Public Goods

A very natural variation of threshold pledge systems like the Street Performer Protocol is a fixed fee mechanism with average cost prices. In this section I will present the theory behind this mechanism, before turning to its practical implementation (and a practical example!) in the next section.

The basic idea is very straightforward:

1. Everybody interested in a given project makes a pledge, saying they are willing to contribute a certain amount of money to funding the project. If somebody is not interested in contributing that just don’t pledge anything.
2. After all pledges have been made, we distribute the costs of the project equally among as many people as possible: Everybody pays exactly the average cost of the project, as long as they pledged at least as much. More precisely, we figure out the smallest price $p$ such that if everybody who pledged at least $p$ pays exactly the price $p$, then the costs of the project are covered exactly. Nobody pays more than $p$ and if somebody pledged less than $p$ they don’t have to pay anything.
3. If there is no such price $p$, for example because people pledged too little, then the project is not funded and nobody pays anything!
4. In case the project is funded, the money raised is used to create the public good. But only those people who paid get access to the public good! (Here we assume that the public good in question is excludable.)

Points 1 and 3 are very similar to the Street Performer Protocol (SPP) and what happens on Kickstarter. Point 2 is crucially different, as in the SPP and on Kickstarter everybody pays what they pledged and not the price $p$. Point 4 is what happens in many projects on Kickstarter, as I observed in my last post, but it is very different from the idea behind the SPP, which was intended to fund pure public goods without use exclusions. There is another vital difference to what happens on Kickstarter that will become clear in the next section.

The fixed fee mechanism with average cost prices has crucial theoretic advantages:

• Everybody has an incentive to pledge exactly what the project is actually worth to them. The technical term for this incentive compatibility. Note that the SPP is not incentive compatible: there, people have an incentive to understate the value the project has for them, in order to pay less. (This is called “free riding” in the public goods literature.)
• Nobody is forced to contribute anything if they don’t want to. In other words, no matter what happens, after we have used this mechanism, everybody will be at least as well-off as before. This is called individual rationality. Many mechanisms for funding public goods, both practical ones, such as taxation by the government, and theoretical ones, such as the Groves-Clarke mechanism, are not individually rational. But for the private provision of public goods in which people participate voluntarily, individual rationality is essential.
• If the fundraising is successful, we raise exactly as much money as is needed to fund the project. That is, the mechanism not only covers costs but moreover it balances the budget.

Of course this mechanism also has a key disadvantage: We exclude people form using the public good even though the public good could be provided to them at no extra cost. In technical terms we say the mechanism is inefficient. This, however, is unavoidable as there are theoretical results such as the Myerson-Satterthwaite Theorem which says, roughly, that there does not exist a mechanism for the provision of public goods that is incentive compatible, individually rational and efficient. This result tells us that the first best solution of giving everybody access to the public is impossible to attain. The good news is, though, that in face this impossibility result, the fixed fee mechanism with average cost prices is the best possible alternative:

• According to a result by Peter Norman the above mechanism is (asymptotically, in a large economy) the most efficient one among all mechanisms that are incentive compatible, individually rational and guarantee budget balance.
• If the cost of funding the public good is small in comparison to the total size of the economy and the number of people interested in the public good, then the average cost will approach zero. This allows us to get arbitrarily close to giving everyone access to the public good. See also this paper by Martin Hellwig.

Regarding the history of the fixed fee mechanism with average cost prices, I want to mention that average cost prices have been studied for a very long time in the context of monopoly economics and a number of authors have examined fixed fee mechanisms in the context of public goods. However, as far as I was able to find out, the paper by Peter Norman is the first instance where this exact mechanism has been studied in a public good setting.

Of course there is a lot more to say about these results and I plan to write more about the technical details in the future. But today, I want to talk about how this mechanism could work in practice and present a practical implementation which I dub the Average Cost Threshold Protocol.

The Average Cost Threshold Protocol in Practice

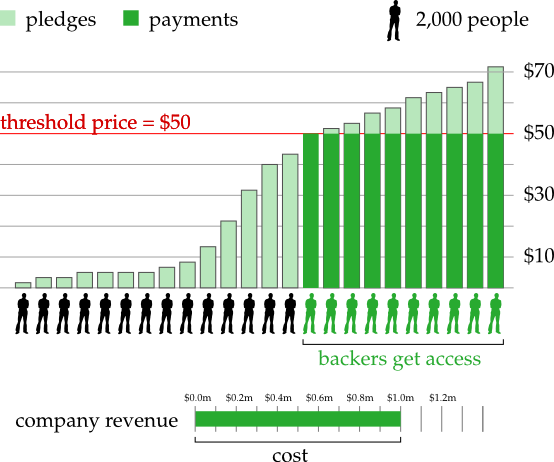
Suppose a company wants to create a computer game and they need money to cover their costs, which total, say, $1 million. They decide to use the above mechanism to raise the funds and so they start a project on a website like Kickstarter which provides all the necessary infrastructure. The project is open to receive pledges for 30 days and at the end of that period the pledges are tallied to see if the project can be funded according to the above rule. (Strictly speaking, setting a deadline is not necessary, but given that many crowd-funding projects raise a large part of their funds the days immediately before the deadline, it seems like a good idea to make use of this psychological effect.)

Many people chip in and pledge various amounts. There are 20,000 people who pledge \$50 or more. So setting a price of \$50 would exactly cover the costs of the game. However, there are only 23,000 people who pledge \$40 or more, so setting a price of \$40 would raise only \$0.92 million which does not cover the costs of the game. Let us assume that \$50 is the lowest price that covers the costs of the game.

Thus, the price is fixed at \$50 dollars. Everybody who pledged \$50 or more now has to pay exactly \$50 dollars. The people who pay these \$50 are now called backers. The total amount raised is \$1 million which covers the costs of the game. This money is used to create the game, and once it is finished, every backer receives a copy.

So far so good. But what about all the other people who would like to play the game? In all likelihood, there are many more people out there who would be happy to pay \$50 to get a copy! Maybe they heard about the project only after the fundraising ended, so they did not have a chance to become a backer. Or maybe they wanted to wait and see how the game turned out before committing to the purchase. Or maybe they did not have \$50 to spare back then, but they do now. Whatever their reasons, it makes perfect sense to provide these people with the public good - we just have to find a way that is consistent with our mechanism.

How do games companies currently do it on Kickstarter? Well, they just sell copies of the game. And the companies keep the revenues from these sales for their own profit. There is nothing wrong with creators making a profit from their work. The problem here is that this breaks our mechanism! Suppose there are another 20,000 people (let’s call them buyers as opposed to backers) who pay \$50 for the game and these revenues are the profits of the company. Now there are a total of 40,000 people (buyers + backers) who have paid \$50 each, which amounts to a total of \$2 million dollars. However distributing the total cost of the game (\$1 million) among 40,000 people would lead to an average cost of just \$25! So, in this scenario, if the company decides to sell the game for profit after it is finished, people would pay twice the average cost, which is very different from what our mechanism specifies.

So let’s suppose we take our mechanism seriously. What would need to happen with the profits from selling the game? Suppose we have 20,000 backers plus 20,000 buyers. As we observed above, distributing the costs of \$1 million equally among those 40,000 people would lead to an average cost of just \$25. But the backers already paid \$50! So here is what needs to happen according to the mechanism: The buyers need to pay just \$25 each. And these revenues need to be given to the backers instead of the company. This makes sure that everybody pays exactly the average cost of the public good.

But now the price of the good has dropped by 50% and the product is gaining ever more public attention. So now there are, say, 40,000 additional people out there who would be willing to pay \$25 for the game. Here is what the mechanism tells us to do: Charge each of the 40,000 newcomers \$12.50 and give the proceeds to the 40,000 people who purchased the game first. This way, everybody just paid \$12.50.

You can now see where this is going:

• As more and more people buy the public good, the average cost of the good drops.
• The price of the good drops, making the good available to more and more people.
• In this process, early buyers are refunded for the high price they paid in the beginning.
• In particular, because of the transfers from late buyers to early buyers, nobody has an incentive to wait with their purchase until prices drop.

All we need for this to work is for the website that coordinates this process to manage these transfer payments. Of course actually distributing money among many different bank accounts whenever a single purchase is made would incur way too much transaction costs. But the website could simply keep track of purchases and how revenue needs to be redistributed and allow customers to withdraw funds every once in a while. The transaction costs could be passed on to backers/buyers directly or could they could simply be financed from the interest the website earns from keeping the payments for some time.

It is also important to note that the infrastructure for pledging available on the website should still be used for sales, even after the product is finished. This way, if the current price for the game is still \$40, people who would be willing to pay \$20 for the product could submit this “bid” on the website. If enough people pledge \$20, the price of the product will actually drop and they will get a copy. The important thing is that people have an incentive to reveal the true price they are willing to pay! This is in contrast to a classical sales context, where customers have an incentive to understate their true valuation to get the company to lower their price.

The Benefits in Summary

The Average Cost Threshold Protocol is a practical mechanism for funding public goods that allow use exclusions. It is an implementation of the well-known fixed fee mechanism with average cost prices, and thus it enjoys many desirable properties:

• It is in everybody’s own best interest to pledge exactly what they are willing to pay. This is true even in hindsight!
• The protocol makes everybody better off. In particular, nobody is forced to pay anything.
• The costs of the project are guaranteed to be covered for the company.
• Among all possible mechanisms with these properties this one is optimal, that is, it creates the most value for society as a whole.

Beyond these theoretical merits, the practical protocol suggested above has a number of additional benefits:

• Prices to the public good are lowered continuously, in order to provide the widest possible audience with access to the public good as quickly as possible.
• At all times throughout the process, everybody has paid exactly the same price for access to the public good. So nobody has an incentive to wait with their purchase for prices to drop.
• In the sales-phase, it is in the interest of customers to bid what they would be willing to pay, even before prices drop. This allows the mechanism to lower prices more quickly, via optimal price targeting.
• Everybody benefits from getting more people to buy access. Even today, backers of crowd-funding projects often provide significant marketing services to their projects through word of mouth, long after fundraising has ended. Using this protocol, backers are not only personally rewarded for this engagement, but they also help to give more people access at lower prices.

Of course this is not the end of the story! There are a number of variants of this mechanism that are worth exploring.

Variations of the Protocol

There are a number of aspects of the basic version of the Average Cost Threshold Protocol presented above which can be improved further.

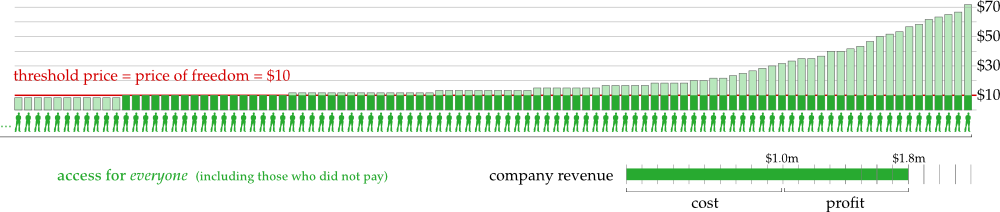
1) Most importantly, the public good provided by the protocol is still subject to use exclusions. We would really like to actually provide a pure public good that everybody has access to, no matter if they paid anything or not. But if we modified the mechanism so that people know the good is eventually going to be provided for free, the economic incentive to contribute something would disappear. Remember, this is the essence of the Myerson-Satterthwaite impossibility theorem!

Nonetheless, there are a number of ways the protocol could be modified to fund the creation of a pure public good without use exclusions. For example, we could set a “reserve price” of, say, \$5 dollars. If the price of the good falls below \$5, the good becomes a pure public good available to everyone for free. Now, of course, everyone who did pay \$5 has paid \$5 too much, which would destroy incentive compatibility in a strict sense. But as \$5 is a relatively small loss, backers who care about the project may very well be ready to accept this loss and gain the warm glow-effect of having made the public good available for everyone. Instead of fixing a common reserve price of \$5 for everyone, backers might also set their own individual reserve price when buying the product. (This of course would require the redistribution scheme to be adjusted.)

A completely different option would be to set a fixed “expiration date” of the use exclusions, for example, three years after the release of the finished product. Buyers would then purchase early access to the product, which is a common business model already today. The difference is that this early access would come with a guarantee that the product will become a pure public good eventually.

Of course such modifications would ruin some of the nice game theoretical properties of the mechanism. But these theorems hinge on the assumption that all backers are entirely rational anyway. And humans are not entirely rational, they are also benevolent and they tend to be tremendously enthusiastic about creative projects they like. So there is room enough for such small changes to work, even if they don’t fit into the rational framework.

2) Companies or creative individuals funding a project using the “vanilla” Average Cost Threshold Protocol as defined above enjoy the tremendous benefit of having their costs covered in advance by payments very similar to pre-purchases. They are not funded through equity and they have no liabilities, which means they have no investors that they need to satisfy through profits and they have no debt that they need to pay off. But that does not mean that all is well.

First of all, after the project is funded and the company received the payment to cover their costs, they are not going to receive any further payments, whatsoever. This means that they have no further economic incentives to make the project succeed. They may have incentives in terms of their creative ambition, their reputation as a company, their individual careers or simply their personal integrity. But the economic incentives to make the product shine, to market it well, to finish it on time and on budget or even to complete the project all - they are all gone. This is clearly not in the interest of anybody! Therefore it is a good idea to allow the company to make some profits in order to create the corresponding economic incentives.

Moreover, no matter how accurately the company projected the costs of the project at the outset, the actual development may run over budget. Projects often (always?) do. So despite the fact that the initial fundraising is expected to cover costs in advance, the company still faces financial risks. To make these financial risks worthwhile to the company, it stands to reason that the company is allowed to make some profit.

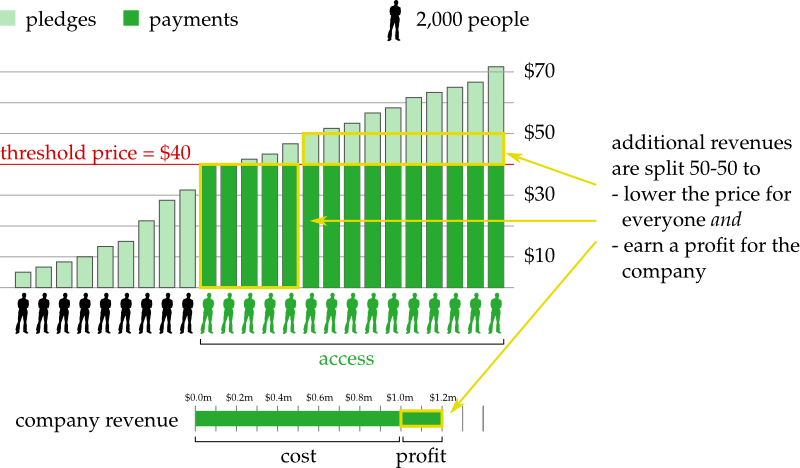
Fortunately it is straightforward to allow the company to make a profit and at the same time allow the public to enjoy decreasing prices. The rule is simple: Half of the payment a new buyer makes goes to the previous backers, the other half is profit for the company. An example. Initially, 20,000 backers paid \$50 each to raise \$1 million. Now, 10,000 additional buyers want access. According to the original protocol, everybody would have to pay \$33.33 now. But instead, we ask the newcomers to pay \$40. Half of that is the profit of the company, which amounts to \$200,000 in total. The other half goes towards refunding the original 20,000 backers so that everybody paid just \$40 in total. In this way, prices will decrease steadily with an increasing number of buyers. But still, the company stands to make an unlimited profit from creating a great product! This amounts to a reasonable compromise between the interests of the company and the social goal of giving access to as many people as possible.

The great thing about this variation is that it preserves many of the nice game-theoretic properties of the original mechanism. In particular, this modified mechanism is still incentive compatible and individually rational. It still covers costs by producing a budget surplus instead of a balanced budget. It is less efficient than before, because fewer people get access for the same amount of money. But still, as the number of buyers grows, the price goes to zero, enabling everybody to afford access if the public good becomes popular enough.

Of course, nobody says that revenues always have to be split 50-50 among the company and its backers. Any other ratio would do. The ratio could change over time. Or each backer could choose their own ratio (similar to what the Humble Bundle is doing), leading to a democratic vote on how revenues should be split. Also, this idea can be combined with the first variation presented above to create a protocol that produces both profits for the company and a public good without use exclusions, provided the good becomes popular enough. In this case the profits for the company are bounded and it is not entirely rational for buyers to reveal their true valuation, but still this promises to be an excellent compromise.

3) From a game theoretic perspective it is important (though not indispensable) that everybody pays the same price. However, from a practical perspective that may not be desirable. Some backers may want to be charged more than other backers. Maybe because they want to show how much they value the project. Maybe the company decides to offer rewards for backers who pay much. Most importantly, there is a real possibility that projects cannot be funded without backers who self-select to pay a very large premium on the average cost. The public interest in the project may not be broad enough to get the costs covered on an average cost pricing basis, but the interest may well be deep enough to cover costs if some people are allowed to pay more.

A special case is the money the company itself puts into the development. Companies and creators running crowd-funding projects often put a significant amount of personal wealth into their projects. Usually, these are funds that do not show up during the fundraising campaign. But an effective mechanism for funding public goods should explicitly incorporate a facility to account for this common practice.

Again there are several ways to allow backers to pay more than the average cost during the initial fundraising campaign. (Note that backers can always pledge as much as they want, but in the original protocol, they will never pay more than the average cost.) One way to accommodate this is via the variable reserve price mechanism mentioned above. Backers who want to pay a lot could simply set their personal reserve price to exactly the same amount as their pledge. Then, they could get charged the entire amount if the fundraising campaign is successful.

However, the above variation would also imply that these backers are not refunded anything. This may well be in the interest of very enthusiastic backers, but it would not fit the needs of the company who wants to recoup the large investment it made into the project in this way. Also there may be backers who are willing to make a very large payment, if the project can’t be funded otherwise, but would like to be refunded if the project turns out to be widely popular in the long run. To accommodate these interests, one could allow backers to specify that they want to be charged more during the fundraising campaign. Later on, the revenues earned from sales of the product could be used to refund backers in proportion to the payment they made during fundraising. This way large backers could eventually recoup their investment if the project is widely successful.

While it may generally not be rational for backers to make such large payments, the presence of this option does not change the fact that for the average backer the protocol remains incentive compatible and individually rational. As before, this variation can also be combined with the variations 1) and 2) mentioned above.

Conclusion

The Average Cost Threshold Protocol and its variations promise to yield an effective mechanism for the private funding of public goods. Even if this particular mechanism is not the ultimate answer, it shows that there is a lot of room out there for improving upon existing crowd-funding mechanisms in this regard. I hope that more people apply their creativity to invent new ways of making the private provision of public goods attractive. In a world where public goods make up an increasing share of the global economic output, such a mechanism could change the way we do business and interact with each other’s creative work.

My latest math paper has hit the arXiv. It is called Enumerating Colorings, Tensions and Flows in Cell Complexes and it is joint work with Matthias Beck, Jeremy Martin and Logan Godkin. It has been great working with all of them. I am particularly pleased that this is my first joint paper with Matthias, the great guy who brought me to San Francisco!

This paper is a continuation of the work that Matthias Beck and Thomas Zaslavsky started on using inside-out polytopes to prove reciprocity results for counting polynomials and that Raman Sanyal and I adapted to the case of modular counting functions. In the present work we generalize all of this considerably, by proving a whole collection of combinatorial reciprocity theorems for flow, tension and chromatic quasipolynomials defined on cell complexes, i.e., in terms of arbitrary integer matrices. The fact that the Ehrhart theory methods developed for the graph case do generalize to cell complexes is a testament to the remarkable power of the geometric approach to combinatorics. Head over here to hear the full story!

In this post, I kick off a series on the private provision of public goods, by taking a good look at Kickstarter and the Street Performer Protocol.

Crowd funding really took off in 2012. From my personal perspective, the most visible embodiment of this trend was the emergence of Kickstarter as a means of funding game development projects. Double Fine Adventure was one of the first projects that brought this concept to public attention by raising $3.3 million. This was quickly followed by the success of such projects as The Banner Saga ($723k), Shadowrun Returns ($1.8m), Star Citizen ($2.1m) and Project Eternity ($4.0m). Of all of these, I think The Banner Saga stands out, as it is a very original project by a comparatively unknown team, whereas the other projects capitalized on well-established concepts and the fame of their celebrity project-leaders.

When I first encountered Kickstarter, I became very excited, not just because of the addictive warm-glow effect of making great projects happen, but also because Kickstarter struck me as the first large-scale, widely popular implementation of the Street Performer Protocol. The Street Performer Protocol is a brand name coined in the 90s by Steven Schear, John Kelsey and Bruce Schneier for a very simple and very old mechanism for fundraising: Artists announce that they will do a public performance if the audience as a whole pays a fixed total amount (or more). If enough spectators chip in to reach this threshold, the artists collect the money and perform. Otherwise, nobody pays anything and there is no performance. This is essentially how Kickstarter operates.

Now, back in the 90s, the Street Performer Protocol (SPP) was heralded as a mechanism for funding public goods. A public good is a good that, once it is created, can be enjoyed by anybody without being “used up”. (See the end of this post for more details on the term.) Software and computer games make excellent examples of public goods in that they can be copied perfectly at a vanishingly small cost.

Commercial publishers of software and games often impose legal and technical restrictions on copying. They create use-exclusions in order to be able to sell the software like a classical private good. While this is a perfectly valid business model, it seems wasteful because it prevents people from using the software who could benefit from it at no additional cost. By contrast, the open source / free software model of software development ensures that free copying is possible, both legally and technically. But if software is to be made available as a public good without use-exclusions, how is its development to be funded? People hoped the SPP might provide an answer to this question, and, sure enough, the SPP soon had important successes. For example, in 2002, Ton Roosendaal managed to raise €100,000 in order to buy the rights to the 3d software Blender (that he created) from the creditors of his bankrupt company NaN and released Blender under the GPL. But despite such isolated successes the SPP did not gain widespread adoption, and cross-subsidies remained/became the primary source of funding for open source software projects.

With all of this in mind, I became very excited when I discovered how successful Kickstarter was. Did we finally have a working way of financing the private provision of public goods directly? My enthusiasm led me to contribute funds to a couple of projects on Kickstarter, which has been a great experience all around. But. This experience also made it clear that, contrary to my first hopes, Kickstarter is not about the provision of public goods and it is not used to implement the SPP - at least judging by the way it is used in the game development community.

None of the games mentioned above are going to be released as a public good when they are completed. Instead, they are going to be sold, with the profit to be shared by the development studio, possible publishers and whatever investors they may have. The Kickstarter backers are not investors in this context. Their pledge is not a contribution towards the creation of a public good, it just buys a single license for a future product and is thus seen as, merely, a pre-order. From this point of view, customers buy a product years in advance that they know virtually nothing about. Moreover they self-select for price targeting by voluntarily paying much more than price of the pre-order. (This price targeting is significant. All aforementioned projects had individual backers pledging more than $10,000 dollars and a significant percentage of backers pledged more than double the price of the respective pre-order.) In exchange for these additional funds, they get additional merchandise of limited value and the warm-glow effect of being part of a project they care about.

To be sure, this long-term pre-order model of funding games does potentially have great positive effects. When an audience not only buys the product but funds the creation process from the start, stakeholders become the key financiers of the project, which may lead to fewer conflicts of interest. Development teams achieve greater creative independence, they can follow their instincts and have to worry less about mass market appeal and investor interests. In the most optimistic scenario, this can lead to a more satisfying experience, both for the developers and for the customers.

Nonetheless, treating a Kickstarter pledge as a “pre-order” sounds just wrong to me, for several reasons. First of all, backers take on a large amount of risk with their pledge. They have no guarantees that the product is going to be delivered, they have no influence on the creation process, they have no information about the product they are buying, the price they pay is, on average, way above the final market price of the product, and they receive none of the revenues made by selling the final product. In short, if Kickstarter is used to create software that is going to be sold for-profit, then backers make a huge investment, reap none of the profits that arise from their investment, carry a large share of the risk, and end up paying much more than customers who buy the product after it has been released.

To be clear: I do think that all of the aforementioned projects are run by development studios with the best intentions. And while contributing on Kickstarter does have a warm-glow effect that can be addictive, I am convinced that most backers are rational in their decision. The huge transfer payment from backers to developers inherent in the pre-order funding model described above is a deliberate decision to fund art that would not be created without such a payment. But for studios to dismiss this huge gift as a pre-order and then to sell the resulting product exclusively for their own profit strikes a wrong chord with me.

Now, the pre-order model is certainly not the only way Kickstarter is used. The are projects, such as Chris Granger’s wonderful Light Table project, that were created with the explicit purpose of producing open source software. The Light Table Kickstarter project raised $316,720 and makes a prime example of the use of the Street Performer Protocol for funding a public good. I do hope that other Kickstarter projects will have the courage to ask backers for money, even if they pledge to make their final product open source upon release. In my view, this would be a much fairer deal. Projects such as LightTable (and Blender ten years ago) show that this can work, despite the fact that it is not rational in a strict economic sense for an individual backer to donate money to such a development project. If this mode of using Kickstarter catches on, we will have a truly new way of financing public goods. Such a mechanism would have a huge impact, given that an ever-growing share of the global economy deals in virtual goods that could in principle be turned into public goods.

So, I do still have hopes for more public good projects on Kickstarter. But hope is not good enough!

Therefore, I will use this post to kick off a series of posts on the economics of public goods, dealing with questions such as: What other mechanisms for funding public goods are out there? What tools do we need to analyse such mechanisms? What are the theoretical limits? How would a funding platform for the private provision of public goods have to work in order to be widely successful?

Addendum: One paragraph introduction to public goods. A public good is a good that, once it is created, can be enjoyed by anybody without being “used up”. Anyone can stand by and watch a street performance, once it is happening. Anyone can walk on a street, once it is built. And anyone can make a copy of a digital movie, once it has been created, without anyone having “less” of the movie. Of course this is not quite true. A performance may become too crowded for new arrivals to see anything, and a street may become too congested for anybody to walk or drive. So, under extreme conditions there is some rivalry in the consumption of these good, but in most cases one more onlooker or one more pedestrian does not “cost” anything, which makes these goods non-rival. Now, as far as digital movies are concerned, their copying is perfectly non-rival as both copies are identical and nobody has “less” of the movie. However, there are often many legal and technological barriers in place to prevent consumers from copying. That is, the industry tries (with moderate success) to exclude consumers from obtaining a copy the movie, if they did not pay for it. When these restrictions are not in place, there is nothing preventing a consumer from making a copy, and the movie becomes a public good without use-exclusions. A pure public good is perfectly non-rival and non-excludable. In practice, public goods often have some limited rivalry, but it may still be instructive to think about them as public goods as they are non-rival in most cases. For my purposes, I do not include non-excludability in my definition of a public good, as the role of use-exclusions in the funding of public goods is precisely what I want to discuss.

The large-scale formalization of mathematics has been a long-time dream of many. Personally, I would love to accompany every mathematical research article I write with a formal version, including formal proofs, and I think widespread formalization is important for the mathematical community in general.

However, as long as current automatic proof systems are unable to do even high school mathematics on their own, this dream will not turn into reality. Yet, we do not need to wait for automatic proof systems to get better. On the contrary, there is something that we can do now that will help both the formalization of mathematics and the improvement of automatic proof systems:

We need to create a standard file format for formal sketches of mathematical articles.

In the rest of this post, I will explain what I mean by this and why I think this is useful. Note, however, that these ideas are very much a work in progress. Also, I should say that my perspective is that of a mathematician working in discrete geometry and combinatorics. I am not a logician and I am no expert in interactive or automatic theorem proving, and I have begun to explore the world of formal proof systems only recently. Nonetheless, I think that the one thing that could make writing formal mathematical proofs more accessible to a working mathematician like me is a standard file format for formal sketches of mathematical articles.

Formal Sketches

With a mathematical article I mean an informal mathematical article on some topic of current research interest, as might be found in a journal or on the arXiv. With a formal sketch I mean a formal version of such an informal mathematical article with the following properties:

• A formal sketch contains the definitions, theorems and proofs given in the informal mathematical article.
• The formal sketch is human-readable and human-writable.
• Moreover, reading or writing a formal sketch of an informal mathematical article should not be significantly more difficult than reading or writing the informal article itself.
• Definitions and theorems in the formal sketch are given in a fixed logic without any ambiguity.
• Proofs in the formal sketch are formal proof sketches in the following sense: A formal proof sketch is not a complete formal proof and it is not a human readable representation of a given formal proof. Instead, a formal proof sketch serves as advice for constructing a formal proof by breaking the task of constructing a formal proof down into smaller, easier steps. The purpose of a formal proof sketch is to help an automatic proof system to construct a complete formal proof.
• Formal proof sketches are independent of any particular automatic proof system and any fixed library of definitions and theorems. Formal sketches of mathematical articles follow a decentralized open-world approach to formalizing mathematical theory.

I do not claim that current automatic proof systems will actually be able to construct a formal proof from a formal proof sketch. This goal may still be many years away. Current automatic proof systems will still require additional prover-specific human help to construct formal proofs. Nonetheless, I argue that it is still beneficial to create a standard file format for formal proof sketches now.

The creation of a standard file format for formal sketches of mathematical articles will, I hope, accomplish two things:

• A standard file format for formal sketches of mathematical articles will make it more attractive for everyday mathematicians to formalize their mathematical articles. This will facilitate the creation of a large body of formalized real-world mathematics. Moreover, this effect will become more pronounced as automatic proof systems become more powerful.
• A standard file format for formal sketches of mathematical articles will encourage competition between automatic theorem provers and innovation in automated reasoning. Formal sketches may serve as a benchmark for comparing the capabilities of different provers. The availability of an interesting set of formal proof sketches will also make improvements in the automated reasoning capabilities of current provers more relevant.

These two effects mutually reinforce each other. This has the potential to create a positive feedback loop that will help the large scale formalization of mathematics to take off, finally.

Of course, a large effort will be required to get this process going. One means of bootstrapping this process may be the creation of a supplemental file format for the annotation of formal proof sketches with prover-specific advice. Nonetheless, I think that the creation of such an ecosystem is possible and that the potential benefits justify the effort. As outlined above, the foundation of this system is a standard file format for formal sketches of mathematical articles.

In the remainder of this post I will discuss how such a standard file format might look like.

What file formats are out there already?

Fortunately, there is already a rough consensus on what a formal, human-readable, declarative language that resembles ordinary mathematics should look like. Many people tried to come up with their own version of such a language and, independently, they arrived at essentially the same result, a common mathematical vernacular. This argument has been made by Freek Wiedijk in a wonderful article where he compares the languages of the Hyperproof, Mizar and Isabelle/Isar systems and points out the common structure behind their differences in surface syntax. His miz3 syntax for HOL Light is another example of this mathematical vernacular.

This mathematical vernacular is a format for formal proofs with a very precise meaning. Formal sketches, on the other hand, should live at a higher level of abstraction. In particular they should be intentionally vague in specifying how, exactly, to prove “the next step” in a declarative proof. Freek has introduced the notion of a formal proof sketch and given some very nice examples. A formal proof sketch, in his sense, is an abbreviated version of a full formal proof in the Mizar language, in which some intermediate steps and justifications have been removed. It turns out that using such abbreviations, one can arrive at a document that is very close to a natural language version of the proof and that still accurately reflects the structure of the underlying formal proof. A formal proof sketch is correct if it can be extended to a formal proof in the Mizar language just by adding labels, justifications and intermediate steps.

Freek intends formal proof sketches to serve only as a means for presenting a formal proof. He expressly does not intend formal proof sketches “to be a ‘better way’ of writing formal proofs”. In this post, however, I use the terms “formal sketch” and “formal proof sketch” with the explicit intent of employing these sketches as a tool for authoring and archiving formal proofs.

In the context of this prior work, a formal sketch in the sense of this post would be the following: A document containing definitions, theorems and proofs, where the proofs are written in an abbreviated version of the mathematical vernacular. Such a document would be correct, if the proofs can be extended to full formal proofs in the mathematical vernacular by adding labels, intermediate steps and additional justifications. Such a formal document would not serve as an abbreviated representation of an underlying formal proof. Rather, it would serve as formal but ambiguous and incomplete advice to the (human or machine) reader for constructing a formal proof.

The purpose of creating a standard file format for formal sketches based on the mathematical vernacular is to share formal sketches across different proof systems. In this regard, the OpenTheory project has done vital pioneering work. The OpenTheory article format is a low-level format for encoding proofs in a fixed logic. This file format can be read, written and interpreted by several different provers. The OpenTheory article format is prover independent in the sense that in order to use the proofs contained in an OpenTheory article, a prover only has to use a version of higher order logic that can simulate the primitive inference rules defined in the OpenTheory article standard. OpenTheory demonstrates that sharing of proof documents among provers is possible. The creation of a standard for formal sketches of mathematical articles would aim to do the same at higher level of abstraction.

OpenTheory achieves prover independence by compiling prover-specific proof tactics down to elementary inferences. The only way to achieve prover independence at the high level of abstraction that formal sketches aim for, is by removing all prover-specific tactics and library-specific references from the justifications of the declarative proof steps. (Incidentally, this removal of justifications is also Freek’s key step in converting a declarative formal proof into a formal proof sketch.) In this way, the higher level of abstraction is “bought” at the cost of introducing ambiguities into the formal proof sketch.

In terms of previous work, a standard for formal sketches of mathematical articles could thus be described by the slogan “OpenTheory for formal sketches of Mizar-style articles”. In the next section, however, I want to change tack and describe the properties a format for formal sketches should have, by drawing analogies to informal mathematical articles as they are used today. In particular, I will argue that informal mathematical articles are successful precisely because they are ambiguous.

What properties should the file format have?

The research articles that mathematicians all over the world write every day have several astonishing properties. Compared to most other texts humans write, even in the sciences, mathematical articles are extremely formal. Yet, compared to formal proofs in the sense of proof theory, mathematical articles are extremely informal, ambiguous, imprecise and even erroneous. There are three aspects of this inherent ambiguity of mathematical articles that I want to call particular attention to.

• Even though mathematical articles build on a huge amount of previous results, they manage to refer to this huge body of knowledge without becoming too verbose. This feat is achieved by three means: Mathematical articles typically 1) assume background knowledge on part of the reader, 2) include brief preliminary sections that summarize the most important parts of the required background knowledge, and 3) state the most important previous results they draw on as explicit theorems.
• Mathematical proofs are written in a declarative rather than in a procedural style. They consist of a sequence of true assertions, rather than a sequence of instructions on how exactly to get from one assertion to the next. This allows readers to make use of their own background knowledge and understanding of the subject matter and avoids a commitment to any particular set of rules.
• To make sense of a mathematical article in all its details requires an often significant effort on the part of the reader. Every mathematician has been in the situation of spending hours trying to understand a step in a proof that was (apparently) obvious to the author. This is made necessary by the previous two properties of mathematical articles mentioned above.

All three of these properties make mathematical articles more successful at communicating mathematical ideas. Mathematical articles would be less readable today and completely unintelligible 50 years from now, if they were extremely verbose, required the reader to refer to a particular textbook while reading and forced the reader to follow exactly the same train of thought the author used.

I think there is something we can learn from this:

Mathematical articles have been successful at communicating mathematics in the last centuries precisely because they are ambiguous. Formal mathematical articles have to embrace this ambiguity if they are to become successful.

Concretely, this has the following implications for a formal format for mathematical articles.

• Formal mathematical articles have to avoid binding themselves to any particular library of theorems or any particular proof system.
• Formal mathematical articles should be written in a declarative style.
• Formal mathematical articles have to place the burden of working out the details on the reader, no matter if the reader is a human or an automatic proof system.

These general considerations point to a declarative format for formal proof sketches in the Mizar style in which the explicit references to external theorems and prover specific tactics have been removed as far as possible.

From a pragmatic point of view, the removal of most explicit references to libraries and provers from formal sketches has two huge advantages for mathematicians wanting to formalize their articles:

• Mathematicians do not have to learn a (huge) dictionary or “API” to get started with formalization.
• Mathematicians do not have to fear that their formal sketches will become unreadable when the current generation of provers becomes obsolete.

These two factors, the tie-in and the steeper learning curve associated with binding a formal sketch to a particular API, are the two factors that keep me personally, as an everyday mathematician, from starting to formalize my research. (The danger that formal proofs break as prover technology changes is particularly problematic.) The removal of these two deterrents would, I hope, make formalization attractive to many other mathematicians as well.

The ingredients of a specification

So far, these are blue-sky ideas and it is way to early to try to turn these into an explicit specification of a formal sketch format (FSF). But, to get the ball rolling, I want to list some ingredients for such a specification that, I think, will be important for success, based on the above considerations.

As explained above, the starting point for FSF is a Mizar-style declarative proof language in the spirit of the mathematical vernacular. Proofs in FSF are abbreviated by omitting intermediate steps and in particular justifications. Prover-specific justifications are not allowed in formal sketches at all. To make FSF work, this basic concept should be extended in the following ways.

First of all, as this whole idea revolves about creating a cross-prover file format, close integration with OpenTheory is desirable. In particular:

• FSF should use the same logical foundation as OpenTheory.
• The packaging mechanism should be essentially the same as in OpenTheory. An FSF article imports theorems as axioms and promises to produce a bunch of new theorems as a result (if the reader/prover is clever enough). Note that while the set of exports is uniquely determined by the FSF article, the set of imports is not uniquely determined by the FSF article, but depends on the reader/prover as well.
• The benchmark for whether a prover $P$ “understands” formal sketch $S$ should be this: Is $P$ able to transform $S$ into an OpenTheory article $O$ on its own? $O$ is not uniquely determined by $S$, in particular its imports may depend on $P$. However, all imports of $O$ should be available in $P$’s library.
• FSF should have built-in support for citing theorems from the OpenTheory library.

The formal sketch format should not tie itself to OpenTheory exclusively, however, as independence of any particular system is crucial for the success of FSF. Instead:

• FSF has to embrace an open-world model.
• FSF has to allow all kinds of references to mathematics outside of a given formal sketch article, including references to theorems that are ambiguous or not machine-readable. Examples include:
  • informal citations of an informal mathematical source, like “Proposition 2.1 in Herbert Wilf, generatingfunctionology, 3rd Edition”,
  • explicitly stated theorems,
  • references to open libraries such as Isabelle’s Archive of Formal Proofs, and even
  • free format URLs.

It is important to note that automatic systems processing FSF should not be required to make sense of any of these. A mathematician does not check all references cited in a given article either.

As mentioned before, current provers will probably not be able to “understand” any interesting formal sketch at this time. While the hope is that provers will achieve that goal at least for some formal sketches in the not too distant future, there is definitely going to be a transition period in which provers need additional advice to cope with a given formal sketch. To this end, a supplemental file format for annotating FSF articles should be developed.

• An annotation file $A$ for an FSF article $S$ will consist of prover-specific advice for some steps of the proofs contained in $S$.
• There can be many annotation files for any given article $S$. Different annotation files may give contradictory proof advice.
• It is important that annotations reside in different files than the sketch $S$ itself, so that annotations may be changed, extended or removed while keeping $S$ fixed. Also, this prevents $S$ from becoming unnecessarily verbose.
• As explained above, FSF articles should have explicit justifications only in places where humans would mention these justifications in informal mathematical articles. However, independently of the number of justifications, FSF articles can be made easier for provers to “understand” if they contain many small intermediate steps. While these small steps may be very useful in early FSF articles, they pose the danger of making an FSF article less readable for humans. Therefore:
  • It should be possible to move these “small steps” into annotation files.
  • In the case that these “small steps” are kept in the formal sketch itself, the file format should contain hints indicating which parts of a proof should be “hidden” or “folded” at a first reading.

The goal is of course to progressively remove annotations as provers become more powerful, until the annotations can be omitted entirely.

People tend to have very strong opinions about the surface syntax of any data format. As Freek pointed out, even the different variations of Mizar-style file formats that are out there attach different meanings to the same keywords. Therefore:

• The FSF specification should fix one data model for formal sketches.
• FSF should allow for different serialization formats of this data model.
• The FSF specification should provide at least two different serialization formats:
  • a Mizar-style plain text serialization for human editing, and
  • a plain text serialization that lends itself to easy machine processing (using JSON, XML or Lisp-style S-expressions).

The formal sketch format needs to be supported by a convenient infrastructure. In particular, it will be useful to create

• an open repository for formal proof sketches, and
• standard interfaces for processing a proof sketch plus annotations with the most popular provers.

One might even imagine facilities to “mix-and-match” provers: Use HOL to do the first step in a proof, use Isabelle for the second and have both produce low-level output in OpenTheory format in the process. But of course the realization of such fancy ideas is even further off than a basic version of FSF. Which brings me to the conclusion of this post.

Next steps

Where to go from here? Before trying to go for a formal specification, a proof-of-concept is needed. Therefore, I plan to do the following:

• Create a rough draft of a formal sketch format and an accompanying format for annotations.
• Convert a couple of Freek’s formal proof sketches into this formal sketch format.
• Implement a basic interface for compiling the example sketches plus annotations into OpenTheory articles - for two different provers.
• Create annotations so that the formal proof sketches actually compile with these two different provers.
• Begin experiments on how the provers in question can be improved to do these same proofs with fewer annotations.

At that point, we will have a clearer idea of how the formal sketch format should look and what needs to be done to get this positive feedback loop of more prover-independent formalized mathematics and more powerful automatic provers going.

Comments on these ideas and help in this process are very welcome!