Last week, I attended the IMA Workshop on Geometric and Enumerative Combinatorics which was, hands down, the best conference I have ever attended. The speaker lineup was simply amazing and I return brimming with ideas for future projects and collaborations. I felt, therefore, particularly honored to be invited to speak in front of this audience, given that so many of my personal “academic heroes”, who I have cited so often, were present.

Given these high stakes, I am delighted to say that the talk went very well and that the reception was overwhelmingly positive! I spoke on joint work with Brandt Kronholm and Dennis Eichhorn on a geometric approach to witnessing congruences of restricted partition functions. The great thing about this subject is that it allowed me to do what I love the most about mathematics: using geometric insight to visualize combinatorial objects in an unexpected way. In this case, this approach allowed us to - quite literally - look at partitions from a new point of view and derive new theorems as a result of this shift in perspective.

Accordingly, the talk is very rich in visuals. I always think talks about geometry should put pictures before text. This time around, I went even further than I usually do and created interactive 3d graphics to illustrate the ideas. (See more on the technology below.) This turned out to be a big amount of work, but it was, I feel, well worth the effort. Especially in complex mathematical illustrations, interactivity, animation and 3d can transport much more information in a short amount of time than a static picture (or a bunch of formulas) ever could.

Slides and Video

• Slides. You can view the slides online. They require a modern browser and were designed to work on my system on the day of presentation. They may or may not work on your system today. Recommended window size for viewing: 1024x768 pixels. Use arrow keys to navigate. Also, the IMA hosts a ZIP archive of the slides for offline viewing - beware, though, that it may take some fiddling to run (see README.txt).
• Video. Happily, the IMA made a video recording of my talk in Minnesota. It turned out very well, except for the fact that the colors are very much off. But you should still be able to make sense of everything.

Title and Abstract

Oh yes, title and abstract, I almost forgot. Who needs those, anyway, when you got slides and video? Nonetheless, here are title and abstract from the Minnesota-version of the talk:

Combinatorial Witnesses for Congruences of Restricted Partition Functions via Ehrhart Theory

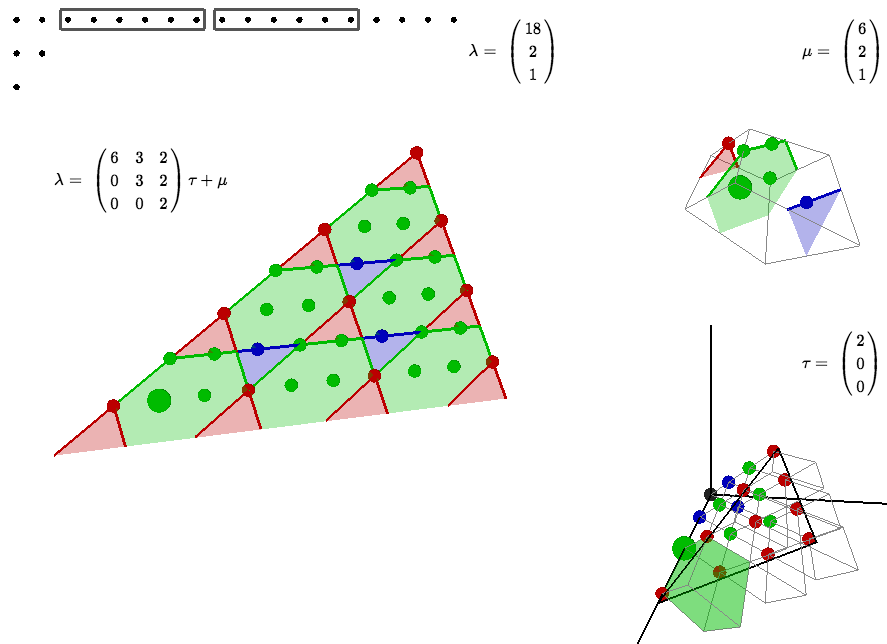
Abstract. The restricted partition function $p ( n,d )$ which counts the number of partitions of $n$ into parts of size at most $d$ is one of the most classic objects in combinatorics. From the point of view of Ehrhart theory, $p ( n,d )$ counts integer points in dilates of a $( d-1 )$-dimensional simplex.

In this talk we use this geometric point of view to study arithmetic progressions of congruences of the form $$ p ( s \cdot k+r,d ) \equiv 0 \mathrm{mod} m \forall k \geq 0. $$ Motivated by the work of Dyson, Andrews, Garvan, Kim, Stanton and others on the general partition function, we are not interested in arithmetic proofs of such congruences, but instead ask for combinatorial witnesses: To show divisibility we want to organize the set of partitions into disjoint cycles of length $m$.

It turns out that geometry is an excellent tool for constructing such combinatorial witnesses. Ehrhart theory induces a natural tiling of the partition simplex that can be used to construct natural cycles in several different ways. Following this approach we obtain combinatorial witnesses for several infinite families of arithmetic progressions of congruences. Moreover, these cycles have a direct interpretation on the level of combinatorics, which leads us to a new type of decomposition of partitions with great potential for further applications.

Finally, one of the great benefits of the application of geometry to combinatorial problems is that one can draw pictures. Instead of using Ferrers diagrams to visualize one partition at a time, we can use the theory of lattice points in polytopes to visualize all partitions of a given number simultaneously and gain insight from their spatial relationship. In this talk, we will therefore take a very visual approach to the subject and present a new way of “looking at partitions” – literally.

This talk is about joint work with Dennis Eichhorn and Brandt Kronholm.

Past Shows

I presented some version of these slides at several occasions:

• Workshop Geometric and Enumerative Combinatorics, IMA, University of Minnesota, Nov 13th, 2014.
• Seminar, University at Albany, Nov 5th, 2014. (presented together w/ Brandt Kronholm)
• Partition Seminar, Penn State, Nov 4th, 2014. (w/ Brandt Kronholm)
• 73rd Séminaire Lotharingien de Combinatoire, Strobl, Sep 9th, 2014. (w/ Brandt Kronholm)

Technology

The slides are made using HTML and JavaScript (or, more precisely, CoffeeScript). The basic slide infrastructure is provided by deck.js and the mathematical typesetting is courtesy of MathJax.

The most important part are obviously the graphics. They are all hand-written using Three.js, which is a terrific library that I have blogged about before. The graphics are all implemented on a very low level and could use a couple of layers of abstraction. I am looking forward to trying out MathBox in the future, which unfortunately is between versions right now and so was not an option.

Let me emphasize that the slides should absolutely not be used as a template. They are hacked together on a very tight schedule using copious amounts of copy-and-paste and an excessive neglect of refactoring. I provide these slides so that you 1) can learn about my research, 2) are inspired to communicate your research visually and 3) start writing your own presentations from scratch, using an appropriate library. I might also be willing to contribute to a library for making math presentations – if you are interested in creating such a library, feel free to get the ball rolling and send me a message!