The mathematical community is discussing how we can leave the journal publishing model behind us. However, putting journals online, making them open access or even leaving them behind us entirely will not solve the challenges the mathematical sciences face in the next couple of decades. A couple of weeks ago, Peter Krautzberger captured this point of view with the simple and beautiful slogan:

Not beyond Journals, beyond Papers.

I agree! And I would like to go one step further. We have to go beyond journals. We have to go beyond papers. And we have to go beyond that which we, as mathematicians, hold dearest:

We have to go beyond theorems!

In this post, I want to make an argument why, from my point of view. This is going to be a long post, but I will try not to rant too much.

The number of new results per year is increasing

The number of mathematical articles - and theorems! - published each year has increased dramatically in the last decades. To give you just one piece of evidence, here is a graph of the number of new research articles entered in the Zentralblatt MATH index each year. This figure is taken from Bernd Wegner’s article in the June 2011 newsletter of the European Mathematical Society.

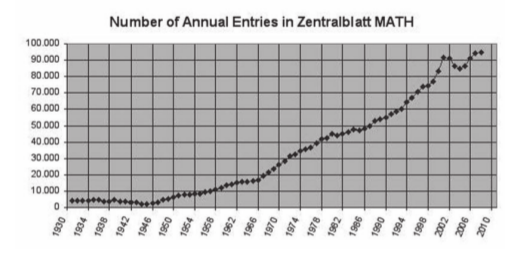
This trend will continue. The human population on earth is increasing and (on average) becoming more prosperous. So, more people will pursue an academic career and more people will become research mathematicians. And, because new theorems are the currency in which mathematicians currently measure research activity, this means that the number of new (!) theorems proven each year will continue to increase dramatically - unless we change our way of thinking about research.

This increase is a loss for everyone

There are roughly 100,000 mathematical articles on the Zentralblatt index that have been published in 2010. One hundred thousand articles, of which the majority contain (supposedly) new results. I’d go so far as to say that most mathematicians cannot read and properly digest more than 100 articles per year. (For me personally, the number is certainly lower than that.)

This means that most mathematicians cannot even make use of 0.1% of the new results published each year.

This must have at least one of the following two consequences. In my opinion, it has both.

Mathematical research is becoming more and more specific.

Mathematicians have a great talent for inventing ever more particular fields and sub-fields and sub-sub-fields in which we can discover ever more new theorems. If this strategy is successful, then these theorems are truly new and they have never come up in another area before. The flip side of the coin is of course that the majority of these very particular theorems will simply not be relevant for most mathematicians (and they will be utterly irrelevant for the rest of the world). A favorite objection to this argument is that, a couple of decades down the road, these results will become relevant in other fields and that results from today will be made use of then. But how is this supposed to happen if mathematicians can only read less than 0.1% of what is published this year? It is much more likely that mathematicians who, 20 years later, arrive at an equivalent problem in another field will simply solve it again on their own. Which brings us to the other consequence.

Mathematical research is becoming more and more redundant.

Independent rediscoveries of theorems happen all the time. They may happen more or less simultaneously. Or they may happen a couple of years apart. Or they may happen in entirely different fields, in which case it may take a while for people to notice that these results are, in fact, equivalent. Whatever form these redundancies take, their number is going to increase.

One can make the argument, that this is no problem at all. Science is redundant. So if all a rediscovery achieves is to make an old result popular in a different time or a different area, then so be it! But this clear eyed view of the world goes against the grain of our current self-image as mathematicians, where only original (never-seen-before) theorems count.

Also, redundancy becomes a real problem in conjunction with increasing specialization. What is the point of doing foundational research in a narrow area of specialization today, if the people who may need this stuff twenty years down the road have no means of discovering it? The only insurance against this type of disaster is to focus on advertising our small corner of mathematics, in the hope that somebody will remember it when the time comes. But again, our mathematical community is not built on this socio-dynamic view of research.

In the end, both trends, increasing specialization and increasing redundance, have the same effect:

Mathematical research is becoming increasingly irrelevant.

Note that I am not saying that mathematics is becoming increasingly irrelevant! There will always be seminal theorems that have a far reaching impact on both mathematics and the real world. But the work of the average research mathematician is going to become increasingly irrelevant.

Unless we finally stop to believe that the only valid form of “research” in mathematics is proving new theorems.

Beyond theorems

I have tried to argue above that the business of churning out as many new theorems as possible is not in the best interest of both mathematicians and mathematics. The two causes that I see as central in this regard are the following.

• We as a community view only new theorems as research. (Thus we create incentives to produce an unnecessarily large inflation of theorems.)
• Our current methods of discovering theorems do not scale with the increase in theorem production.

Thus the best way out of this situation is to acknowledge other forms of mathematical activity as research, not only the proving of new theorems. In particular, activities that help in the discovery of mathematical ideas should be promoted. Here are a couple of suggestions:

Communicating mathematics. This includes all forms of communication, by means of talks, videos, games and of course writing in blog posts, web forums (such as mathoverflow), survey articles and books. This should also include all levels of writing, from expository work for students to references for experts. Finally, this should also include all audiences, from the interested public, to scientists outside mathematics, to mathematicians in other fields and finally specialists in your area. All of these forms of communicating mathematics are widely recognized in the mathematical community. But they are not recognized as research. I argue that mathematicians should get credit as researchers for communicating mathematics, because a larger part of every mathematician’s work will have to be about communication if we are to cope with the present inflation of new results. And we should make it possible that researchers specialize in these social activities, which will only be possible if we give them proper recognition.

Collaborative theorem proving. Instead of everyone trying to get their little theorem published, why do we not try to find new ways of working on the big open questions collaboratively? The polymath projects are very valuable efforts in this regard, but they are only a small first step. As someone on the sidelines of these projects, it appeared to me that in the end, only a relatively small number of people were able to actually contribute to any given polymath project. We have to find ways to make large projects like this asynchronous and distributed. That means, we have to find ways how people can contribute half-baked ideas to research projects, how people who might find them useful can discover them and how to give credit for half-baked ideas in the mathematical community. How to solve these problems is wide open, from my point of view.

The two topics of communicating mathematics and “crowd sourcing” proofs have been widely dicussed in the current debate about mathematical publishing. Now on to two points that have received less attention, as far as I know.

Implementing mathematical software. To make mathematical methods discoverable (and useful), it is of tremendous value to have them implemented in software. This applies to algorithms and methods for visualization as well as to such mundane tasks as the development of decent user interfaces. While these may be engineering tasks in many cases, we should recognize them as research, because they are crucial to the advancement of mathematics! Moreover turning all the useful algorithms available in the literature into usable software is a huge endeavour - it just won’t happen without the proper incentives.

Formalizing mathematics. In my opinion, formalizing mathematics is the single one most important thing that needs to happen if we want mathematics to scale. With “formalizing mathematics” I mean a huge process that includes all of the following.

• The development of the languages and tools necessary to make the formalization of mathematical definitions, theorems and proofs feasible for the average mathematician.
• This will have to go hand in hand with the development of automatic proof systems that can automatically “fill in the gaps” present in any research article.
• The creation of an infrastructure that allows formal mathematical articles to be shared and discovered across different proof systems and formal mathematical languages.
• And, finally, the formalization of (almost) all of mathematics.

It goes without saying that this is more than enough work for generations (plural!) of mathematicians. We still have a long way to go in all of the four areas indicated by the four bullet points above. And even though work is going on in all of these areas, this work is not as widely known as it should. Freek Wiedijk was kind enough to give me a brief tour last fall, and I plan to blog about this in the near future.

Here is why I think the project of formalizing mathematics is crucial. We, as humans, cannot cope with the sheer quantity of mathematical output that is going to be produced in the 21st century. So we have to teach computers how to discover theorems for us that are relevant for the questions we are interested in. Otherwise, the work of most mathematicians will disappear into obscurity faster than anyone can be comfortable with.

Communicating mathematics, collaborative theorem proving, implementing mathematical software and formalizing mathematics are of course all closely interrelated. Why should we not dream of composite electronic resources that are accessible and understandable by all kinds of different readers, that we work on collaboratively and that combine expository texts with detailed explanations and usable software with formalized mathematics? This dream is certainly not new and it is shared by many. How should this brave new world of mathematics look like in detail and how do we build it? The process of exploring these questions will be interesting indeed. My point here is that to get there we need to give up the belief that theorem proving is what mathematical research is all about.

The self-image of the mathematician

No matter what happens, proving mathematical theorems is going to become less relevant. If we succeed in changing they way mathematical research works, other activities will become more important. If we do not, the theorems most mathematicians prove will, generally, be redundant and overspecialized. So:

Theorems will become less relevant.

The social and psychological impact of this simple observation is huge. The self-image of the modern mathematician is built entirely on proofs and theorems. We, as mathematicians, grow up on stories of great “heros” who became “immortal” by proving all these great theorems we learn about. Naturally, we aspire to do as they did and so we seek to wrest these eternal truths from the world of pure, abstract ideas that we conquer using nothing but our “beautiful mind”.

Of course I am being ridiculous here, I exaggerate. But our identity as mathematicians is based on the stories we tell each other about other mathematicians - and those stories revolve around theorems and proofs. Often the only thing we know about a mathematician is what theorem they proved and we set up Millenium Prizes to celebrate the act of attaching a particular mathematician’s name to a particular theorem.

The association of “being a mathematician” with “proving a new theorem” is so tight that I have serious doubts about whether we as a community will accept other mathematical activities as research anytime soon. To do so would call into question what a mathematician is at a fundamental level. But this is precisely what we have to do.

Conclusion

The current model of doing mathematics is in need of reform. The fundamental issues with the current model cannot be resolved just by placing mathematical journals on a different economic and organizational basis. The core of the problem is our fixation as a community on theorems and proofs. As these notions are tied so closely to our self-image as mathematicians, finding a new model of doing mathematics is going to be a long and arduous process. But we have to do it, if we want our work to be relevant in a couple of decades.