Since the launch of ChatGPT in November 2022, AI systems have made significant progress. Yet, arguably, no advancement in capabilities since then has made quite as much of an impression on the global public as that launch – and widespread productivity gains have yet to materialize. How will AI develop going forward and at what timescales? Will the real-world impact of AI remain at the level of smart assistants as we use them today? Or will we reach Artificial General Intelligence (AGI), where AI systems can perform any task almost any human can do and act as independent agents in the real world? Will AI advance even further to Artificial Super Intelligence (ASI), vastly exceeding human capabilities in almost all domains?

Instead of making specific predictions, I will argue in this article that all three of the scenarios mentioned above are worth considering in depth. First, there are important conceptual reasons why progress in AI might plateau at the level of AGI or even at the level of AI assistants without advancing further for a prolonged period of time. Second, depending on which scenario materializes, the real-world outcomes will be vastly different, and therefore should be considered separately.

Exponential Growth

Exponential growth is never really a single exponential curve. Rather, it is made up of many sigmoid curves: temporary regimes of rapid improvement that eventually reach saturation and level off, when the technology that spurred the growth gets stuck in ever-diminishing returns. The overall exponential growth trajectory is kept going by another technology taking over, providing the next growth spurt.

A great example of this is Moore's Law. In its general form, it simply states that the amount of compute available per inflation-adjusted dollar grows exponentially. This exponential path of growth has held for over a century across different computation technologies. The specific Moore's Law is a statement about the density of transistors on semiconductors, which in itself has held for 50 years now by virtue of ongoing regime changes in chip manufacturing and design.

In the debate around future growth of AI, much has been made of the question whether the rapid improvements felt after the launch of ChatGPT in late 2022 will continue on an exponential trajectory and whether, to this end, scaling the amount of compute involved will be necessary or sufficient or both.

Scalable Methods

An influential talk titled “The Future of Artificial Intelligence Belongs to Search and Learning” on the role of scale in AI was given by Richard Sutton in 2016. In it he articulates what is known colloquially as the “biggest lesson” or sometimes the “bitter lesson” in AI circles: Scalable methods always win in the long run.

In AI, a scalable method is a method that can use arbitrary quantities of computation and its performance improves proportionately to the amount of computation used. These methods in particular beat “smart” methods that have a lot of domain specific knowledge or structure built-in. Instead of going after one-off gains that can be achieved by hand-crafting a particular human insight into the method, find a general methods that can scale with compute. This will take longer, but the method will benefit from Moore's Law in the long run and eventually overtake hand-crafted competitor methods. (Of course in principle you can do both, but in practice, Sutton argues, people prioritise one over the other.)

Sutton goes through many empirical examples for this phenomenon, which I will not reiterate here. I will point out, though, that it is quite easy to find further examples supporting this hypothesis since 2016 – the spectacular success of Large Language Models (LLMs) being the most noteworthy, but including also breakthroughs in Go, Poker and protein folding.

Data and Scale

A key detail in Sutton's definition of scalability is the requirement that the method should be able to use arbitrary amounts of computation to extract further proportional performance improvements. This statement will rarely be true for any AI method in full generality – instead it will be conditional on some assumptions, in particular regarding the availability of data.

Media Data

LLMs, and the transformer architecture in particular, have certainly demonstrated vast ability to scale, beyond what could reasonably be expected when the architecture was invented in 2017. In fact, because it is so effective, this method has already been applied to a significant fraction of all human media ever created. As Ilya Sutskever put it at his NeurIPS 2024 talk, internet content is “the fossil fuel of AI” and “we have but one internet”. The use of human-generated media data to scale on is reaching its limit.

Rule-Based Data

Note that this is in contrast to the narrative proposed by some in 2023, that the methods in use at that time would suffice to reach AGI, all it would take was scale. Instead, the progress made by AI in late 2024 on tasks requiring reasoning, was only achieved by innovative methods combining LLMs with reinforcement learning (RL). Continued progress was not guaranteed by the growth of compute but required a regime change in the algorithms employed.

Most importantly, this regime change leveraged a different category of data: In domains where tasks have a verifiably correct answer, the feedback required for RL algorithms is easy to generate automatically. This applies in particular to mathematics and particular areas of computer science: Proofs of mathematical theorems are hard to find but easy to verify. Games such as chess and go can also be included in this category. The rules of these games generate a vast but finite and perfectly well-defined decision tree, that very large amounts of data can be generated from, for example by letting the model play against itself. For the sake of this argument, I call this type of data rule-based data.

The regime of scaling reasoning models on rule-based data has only just begun. Tremendous amount of progress in this area can reasonably be expected in the short term. This is not without its pitfalls: as Ilya Sutskever points out in the talk, RL will make models more unpredictable, as opposed to models trained solely on media data. While classic LLMs are mainly “stochastic parrots” that replicate human writing patterns, the combined LLM+RL systems are truly optimising towards a reward function, and as such as are much closer to the concept of “AI” that AI existential risk folks have been worried about for decades.

Simulated Data

The issue with rule-based data, though, is that very few domains of human (or more generally real-world) activity are governed by strict rules and have verifiably correct answers. For general artificial intelligence to arrive, other types of data will be needed. One step beyond rule-based data is simulated data: Instead of requiring that we have at our disposal the entire rules of the game or that we can perfectly decide whether a solution is correct, we instead settle for approximately simulating the effect of actions. Most pertinent example of this is placing a robot in a simulated environment. If the simulation can approximate the physics of interactions of the real robot with a real environment well enough, then the system can learn from the simulation without having to go through the slow and expensive process of putting the real robot through real-world exercises. Importantly, not just the number and duration of simulations, but in many cases also their accuracy can scale with compute and thus benefit from Moore's Law.

The downside of this approach is that the model will learn the simulation. The model's real-world behaviour then stands and falls with how accurately the simulation reflects the real world. Simulating the physics of stacking boxes in a warehouse or the behaviour of drivers, cars, and pedestrians in a busy downtown environment is one thing. Simulating the chemistry of cooking, the human body during surgery or the behaviour of toddlers in a nursery is another. Simulating the real economy, financial markets or the global climate yet another. What these examples illustrate is that constructing good simulators can quickly become the limiting factor of AI, not learning. The industry focus on building “digital twins” is motivated by precisely this observation.

Experimental Data

One means of improving simulators, or indeed of gathering data directly, is to conduct experiments. Here, I do not mean computational experiments that can be scaled with processing power by virtue of known rules or simulations. Instead, this means experiments that have to be conducted in the real world. This includes building particle colliders, conducting clinical trials, or trying to successfully land rockets. It also includes, after all the market research has been done and the MVP has been built, just going ahead and actually founding that start-up to see if the business idea really works – an experiment with a sample size of 1.

As these examples show, gathering such experimental data is very slow and expensive. Sometimes, time can be traded-off for cost. Sometimes, increases in sample size can allow arriving at conclusions more quickly. Either way, the time-scale at which experiments operate is positively glacial, compared with exponential growth of compute. In contrast, to rule-based data and simulated data, compute itself does not accelerate the real-world data gathering process in any way. In this manner, experimental data can become a bottleneck for improvement in artificial intelligence in many domains.

Observational Data

Experiments have the advantage, however, that, in principle, they allow to control for confounding variables, to decide the sample size, to design a test specific to the question you are trying to answer. In many real world domains, however, this is not possible, and you are left with simply observing the world and recording what happens as time goes by. Sometimes, this can be sped up by deploying many observers. A great example of this is Tesla's fleet of cars, which have been gathering data relevant for self-driving for over a decade. In other cases, when the subject of interest is planet earth, the world economy, or the global financial market, the only option is simply letting history unfold.

Therefore, observational data can be scaled only to a very limited extent. This applies in particular to observational data that covers rare events, even though these rare events are often the most important to learn from. At the same time, observational data is the most relevant type of data in most domains of human activity.

Scenarios

As discussed, scaling AI capabilities requires both data and compute. Even if compute per dollar continues to scale exponentially in line with Moore's Law, data is subject to different scaling laws. Media data is finite and has already been largely exploited. Rule-based data is the basis of a new growth regime in AI, but limited to certain domains. Simulated data is scalable but depends on accurate simulators, which need to be built for each domain. Experimental data is the gold standard of data about the real world, but expensive to acquire. Observational data is comparatively cheap to record, but scales only with time. Neither experimental nor observational data scale with compute or “intelligence”.

The point of this is that in domains that require experimental or observational data, or the use of accurate simulators, rapid progress of AI system is not guaranteed by virtue of scaling compute. Of course, rapid progress in those domains is still possible: A human brain reaches general intelligence using data that is readily available through embodied interaction with the real world. However, given the data constraints, achieving AGI will require more than just scaling up current AI methods. Breakthrough innovations will be required for AGI and when those materialize is hard to forecast. While we know for a fact (by virtue of our own existence) that achieving what we call “general intelligence” is possible, it is not clear how far and how quickly data limitations will allow AI to scale beyond AGI to ASI.

This leads us to consider the following scenarios.

AI Assistants

In this scenario, AI systems scale fully in the directions opened by media and rule-based data. In particular, AI achieves super-human performance in many narrow domains of expertise, especially those where it is straightforward to define whether the solutions presented by AI are “correct”. This can include breakthroughs in math, computer science, computational chemistry and related fields. It can also include a revolution in medicine, though brilliant new AI methods will not obviate the need for clinical trials, which will take their time.

However, in this scenario, AI does not become fully “agentic” or “general”, due to the limits imposed by experimental and observational data. While AI is smart, in practical use-cases it needs to be supervised by humans, who need to bring their commons sense to bear to sanity-check AI recommendations. Deploying an AI agent in a fully unsupervised manner on any task of true import would require not just 99% confidence that the agent will not make any major mistakes, but, say, 99.9999%. The path to “many 9s”, as this is sometimes called, may prove to be genuinely hard, and only feasible for narrow-domain agents that are engineered one domain at a time.

A good example for this are, again, self-driving cars. The first version of Tesla's “Autopilot” system was released in 2015. Despite Tesla's vast fleet of cars gathering real-world observational data, and immense progress in both compute and algorithms, a fully unsupervised robo-taxi is scheduled to enter production only in 2027 – and it remains to be seen whether this timeline realises. Waymo, taking a very different approach from Tesla, had its first unsupervised robo-taxi ride in 2015, and today, almost 10 years later, its robo-taxi service is still avaliable in only a handful of cities worldwide. This pace reflects mainly the engineering part of the problem. Regulatory approval and deployment around the world will add further delays before this type of unsupervised narrow-domain agent has large-scale real-world economic impact – and this slow process will take its course one domain at a time.

Even though this scenario is the most pessimistic in terms of the growth of AI capabilities, it is in some sense the most optimistic in terms of the economic impact of AI: It implies that in many domains, humans will become vastly more productive by leveraging AI assistants – yet only few humans will be displaced by AI (and gradually), given that human supervision is still essential for an extended period of time. This productivity boom will be deflationary, yet lead to tremendous economic growth in real terms.

Note that because of the ongoing growth in compute per dollar, combined with AI being constrained by the scale of data, in this scenario AI assistants will be very cheap to operate. Any breakthroughs in software or hardware enabling these developments are unlikely to remain exclusive to particular labs with proprietary IP. First movers will have a limited advantage and fast followers will benefit from reduced capex spend.

Last but not least, it should be noted that just because, in this scenario, AGI is not attained, does not mean that there are no risks associated with the deployment of AI assitents. Precisely because of the expected scaling of reinforcement learning, AI assistents will display both superhuman performance in narrow domains and unexpected behaviour, lacking common sense. A dangerous combination.

AGI Agents

The next step up, in terms of AI capabilites, is a scenario where agents that can make reliable unsupervised real-world decisions become a reality fairly quickly. By investing capital in experiments and observational data gathering across a wide range of application domains, and building high-quality simulators for each, AI development overcomes the immediate data bottlenecks. However, compute still grows much faster than data, making AGI agents, once developed, cheap to operate. These AGI agents will be both virtual and physical, with the former likely to arrive first.

This scenario implies a seismic shift in the global economy. Human labour will become truly redundant, in the sense that AGI agents can perform literally any task a human could do more effectively in terms of resources required. (To put this in perspective, a human daily diet of 2,000 kcal corresponds to 2.3 kWh, which, using technology available today, suffices to generate well over 1 million output tokens from DeepSeek R1 70B.) The first jobs to become redundant will likely be those that are screen-based, inexperienced, or rule-driven. More resilient will be those roles that require experience, judgement across multiple domains, or relationships and face-to-face interaction. But eventually there will be no value left for human labour to add, except where humans add value purely by being human. Brain-computer interfaces may change the nuances of this dynamic, but not the fundamentals.

On the one hand, this transformation will make the economy vastly more productive. The more important impact, however, is that, unless a different societal contract is put in place, e.g. granting a universal basic income, the purchasing power of the vast majority of humanty will completely vanish. A utopia is possible where humans spend all their time doing what they desire, caring for and entertaining each other. However making this utopia come to pass will either need massive transfers of capital (through one mechanism or another), or it requires that owners of capital are willing to pay a substantial premium for the privilege of being entertained by and cared for by humans specifically. A distopia is also imaginable where the economies of those who own capital and those who don't detach from one another, creating AI-generated wealth for the former and poverty for the latter. The dynamics will be highly non-linear. The only thing that seems certain is that returns on capital will vastly exceed returns on labour. Comparing this epochal change to the industrial revolution underestimates its impact by orders of magnitude. And this is not even touching upon the possibily that AGI agents might become self-aware, and all this implies.

However, in this scenario, the assumption is still that the capability of AI is limited. AGI agents can surpass humans by a wide margin in narrow domains and are more capable and resource-efficient as a general agent. Yet, ASI – an AI system that outperforms all humans by orders of magnitude in all areas – does not materialize, due to the scaling limitations for most domains discussed above.

ASI

What if ASI does materialize?

Much has been made of the distinction between fast-takeoff and slow-takeoff ASI. The idea behind fast-takeoff being that once AI reaches a level on-par with humans, then AI will be able to start improving itself, leading to a further increase in the pace of AI performance improvements. Of course some kind of self-improvement has been part of Moore's Law for the past century: advances in the previous generation of computers have always been leveraged to design and build the next generation of computers. The new element with ASI would be that, for the first time, humans are taken out of the loop entirely. The constraints of physics and economics remain in place however.

A better question to ask, in my opinion, is: How useful is raw intelligence really? The limitations imposed by experimental and observational data we have discussed already. For example, even with the most brilliant ideas for a grand unified theory of physics, experiments still need to be conducted to attempt to falsify it. There are many other limitations however, including chaos theory (even with a perfect model, to predict the global economy, society, or the weather with perfect accuracy, you need to measure initial conditions with greater accuracy than practically possible), computational complexity (making a Go board just one square larger doubles the complexity of the game), game theory (depending on the game, having unlimited computational power may increase a player's winnings only marginally versus competing players with simple strategies), economics (even with the most brilliant design for a new processor, you still need to build the factories to manufacture it and power plants to run it at scale), and markets (“markets can remain irrational longer than you can remain solvent”, “being right or making money”), to name just a few. In short, the omnipotence that some ascribe to ASI is not a given. The amount of real-world impact of ASI may well scale more with the amount of capital it is allowed to accumulate (or indeed that it is endowed with from the start) than with the magnitude of its intelligence.

However, none of the above obstacles are a guarantee that ASI, if and when it arrives, will not “take off”. Super-intelligence may well provide leverage above and beyond what we can imagine. “Any sufficiently advanced technology is indistinguishable from magic,” as Arthur C. Clarke famously put it. If this comes to pass, then all bets are off. In particular, after this event, humans will no longer be in charge – one way or another. ASI alignment is a real challenge that we have to get right on the very first try – a daunting challenge. The short story Firewall by David D. Levine provides a good sense of the magnitude of this occasion, and I will not spoil here whether it has a happy ending or not.

Last week, I attended the IMA Workshop on Geometric and Enumerative Combinatorics which was, hands down, the best conference I have ever attended. The speaker lineup was simply amazing and I return brimming with ideas for future projects and collaborations. I felt, therefore, particularly honored to be invited to speak in front of this audience, given that so many of my personal "academic heroes", who I have cited so often, were present.

Given these high stakes, I am delighted to say that the talk went very well and that the reception was overwhelmingly positive! I spoke on joint work with Brandt Kronholm and Dennis Eichhorn on a geometric approach to witnessing congruences of restricted partition functions. The great thing about this subject is that it allowed me to do what I love the most about mathematics: using geometric insight to visualize combinatorial objects in an unexpected way. In this case, this approach allowed us to - quite literally - look at partitions from a new point of view and derive new theorems as a result of this shift in perspective.

Accordingly, the talk is very rich in visuals. I always think talks about geometry should put pictures before text. This time around, I went even further than I usually do and created interactive 3d graphics to illustrate the ideas. (See more on the technology below.) This turned out to be a big amount of work, but it was, I feel, well worth the effort. Especially in complex mathematical illustrations, interactivity, animation and 3d can transport much more information in a short amount of time than a static picture (or a bunch of formulas) ever could.

Slides and Video

• Slides. You can view the slides online. They require a modern browser and were designed to work on my system on the day of presentation. They may or may not work on your system today. Recommended window size for viewing: 1024x768 pixels. Use arrow keys to navigate. Also, the IMA hosts a ZIP archive of the slides for offline viewing - beware, though, that it may take some fiddling to run (see README.txt).
• Video. Happily, the IMA made a video recording of my talk in Minnesota. It turned out very well, except for the fact that the colors are very much off. But you should still be able to make sense of everything.

Title and Abstract

Oh yes, title and abstract, I almost forgot. Who needs those, anyway, when you got slides and video? Nonetheless, here are title and abstract from the Minnesota-version of the talk:

Combinatorial Witnesses for Congruences of Restricted Partition Functions via Ehrhart Theory

Abstract. The restricted partition function $p ( n,d )$ which counts the number of partitions of $n$ into parts of size at most $d$ is one of the most classic objects in combinatorics. From the point of view of Ehrhart theory, $p ( n,d )$ counts integer points in dilates of a $( d-1 )$-dimensional simplex.

In this talk we use this geometric point of view to study arithmetic progressions of congruences of the form $$ p ( s \cdot k+r,d ) \equiv 0 \mathrm{mod} m \forall k \geq 0. $$ Motivated by the work of Dyson, Andrews, Garvan, Kim, Stanton and others on the general partition function, we are not interested in arithmetic proofs of such congruences, but instead ask for combinatorial witnesses: To show divisibility we want to organize the set of partitions into disjoint cycles of length $m$.

It turns out that geometry is an excellent tool for constructing such combinatorial witnesses. Ehrhart theory induces a natural tiling of the partition simplex that can be used to construct natural cycles in several different ways. Following this approach we obtain combinatorial witnesses for several infinite families of arithmetic progressions of congruences. Moreover, these cycles have a direct interpretation on the level of combinatorics, which leads us to a new type of decomposition of partitions with great potential for further applications.

Finally, one of the great benefits of the application of geometry to combinatorial problems is that one can draw pictures. Instead of using Ferrers diagrams to visualize one partition at a time, we can use the theory of lattice points in polytopes to visualize all partitions of a given number simultaneously and gain insight from their spatial relationship. In this talk, we will therefore take a very visual approach to the subject and present a new way of ``looking at partitions'' -- literally.

This talk is about joint work with Dennis Eichhorn and Brandt Kronholm.

Past Shows

I presented some version of these slides at several occasions:

• Workshop Geometric and Enumerative Combinatorics, IMA, University of Minnesota, Nov 13th, 2014.
• Seminar, University at Albany, Nov 5th, 2014. (presented together w/ Brandt Kronholm)
• Partition Seminar, Penn State, Nov 4th, 2014. (w/ Brandt Kronholm)
• 73rd Séminaire Lotharingien de Combinatoire, Strobl, Sep 9th, 2014. (w/ Brandt Kronholm)

Technology

The slides are made using HTML and JavaScript (or, more precisely, CoffeeScript). The basic slide infrastructure is provided by deck.js and the mathematical typesetting is courtesy of MathJax.

The most important part are obviously the graphics. They are all hand-written using Three.js, which is a terrific library that I have blogged about before. The graphics are all implemented on a very low level and could use a couple of layers of abstraction. I am looking forward to trying out MathBox in the future, which unfortunately is between versions right now and so was not an option.

Let me emphasize that the slides should absolutely not be used as a template. They are hacked together on a very tight schedule using copious amounts of copy-and-paste and an excessive neglect of refactoring. I provide these slides so that you 1) can learn about my research, 2) are inspired to communicate your research visually and 3) start writing your own presentations from scratch, using an appropriate library. I might also be willing to contribute to a library for making math presentations -- if you are interested in creating such a library, feel free to get the ball rolling and send me a message!

When you want to prepare your 3D visualizations for publication in print/PDF you typically want to convert them into a vector graphics format. Three.js is a JavaScript library for creating 3D graphics that can be easily used to create vector graphics images in SVG format from 3D visualizations. Here is an example of how to achieve this -- and you can modify the example right in your browser!

The Story

Last year, I created a 3D-visualization of the greatest commond divisor function. Then, a few weeks ago, I wanted to take snapshots of the visualization for inclusion in a research paper I was writing. However, as the research papers was intended for print/PDF publication, I was not satisfied with rasterizing the image (i.e., "taking a screenshot"). I wanted to have a vector graphics version of the image, especially since my visualization consisted entirely of lines. Ideally, I wanted to have the image in SVG format so that I could edit the result in Inkscape, my favorite program for creating mathematical illustrations. Unfortunately, Sage, the computer algebra system in which I had originally prepared the visualization, does (at the time of this writing) not support exporting 3D plots in a vector graphics format. So I had to find a different tool.

Three.js came to the rescue. Three.js is a fantastic JavaScript library for creating 3D graphics in the browser. It is mature, easy to use, has a large community and a creator, Ricardo Cabello, who is extremely helpful. Moreover, I think scientific publishing needs to move away from the PDF as its main medium and start creating web-first publications for the web browser -- very much in the spirit of, e.g., MathJax and Substance. So, getting my feet wet with three.js was certainly a worthwhile investment.

In my opinion, the three.js version turned out much nicer than the original. Just as with the original version, you can modify the code producing the visualization right in the browser. However, in contrast to the Sage-based version, there is no need for clunky Java applets to do the rendering and there is no dependency on a Sage Cell server that benevolently does all the computation for the reader of the blog post -- now, everything happens right inside the reader's browser, which makes these kind of interactive documents far easier to host. And of course, you can now take SVG snapshots of the visualization, which was the motivation for the whole exercise.

So, let's move on to the graphics and code.

The 3D Visualization

Below is a graph of the greates common divisor function. See this blog post and this expository paper for the math behind this picture. Use the mouse to zoom and rotate.

To take an SVG snapshot of this picture, click here: SVG snapshot.

The SVG Snapshot

This is a static SVG snapshot of the 3D image above. The SVG source is shown below. Paste it into an .svg file and open that in Inkscape for editing. This post-processing by hand is extremely useful!

The Code

Here is the code for the visualization. The language is CoffeeScript. Feel free to experiment and change the code. To reload the visualization with the updated code, click: Run!

Naturally, when working on a project of your own, you will want to have the code on your own system. If you want to use this example as a template to start from, feel free to clone my GitHub repository fbreuer/threejs-examples.

The above code uses both the SVGRenderer and OrbitControls which are not part of the standard three.js library but can instead be found in the examples directory of official three.js repository. This also means that they have some limitations. For example, the SVGRenderer does not support all features of the standard three.js renderers and some fiddling may be required.

Next Steps

Of course this is not the end of the story. Inspired by this success, I already have big plans for a next visualization project based on research papers I am currently writing with Dennis Eichhorn and Brandt Kronholm. I also plan to take a closer look at MathBox, which is a wonderful library for math visualization based on three.js.

20 years ago, the QED project set out to create "a computer system that effectively represents all important mathematical knowledge and techniques". Today, as even a cursory glance at the field will reveal, we are still a long way from achieving that goal. Nevertheless, as the excellent talks at QED+20 showed, there has been a tremendous amount of progress. I also enjoyed the workshop because the illustrious range of speakers at the event gave a wonderful overview of the many different perspectives of the researchers in the area.

However, for most of the workshop, I was struck by an odd incongruence between what researchers in the formalization of mathematics are doing and what I, as a working mathematician, would be interested in.

The potential of QED

From my perspective, there are many benefits that a wide-spread machine-processable formalization of mathematics could have. These potential benefits include:

1. Ascertaining correctness of mathematical theorems.
2. Revolutionizing mathematical publishing.
3. Automation of large-scale case analyses and computations in mathematical proofs.
4. Semantic search of mathematical methods and results.
5. Computerized discovery of new mathematical ideas.

The incongruence that I perceived is this:

To me, correctness is the most boring and least important of these benefits. Yet, it appears to be the one thing that the QED community focuses on almost exclusively.

By contrast, the other items are all very interesting and appear crucial to the advancement of mathematics. However, with some exceptions they do not seem to be what current research in QED is all about. Let me explain what I mean by that by addressing these items one by one.

Correctness

Mathematical research has two different modes: On the one hand, there is the “hot phase” of research (as Bruno Buchberger likes to call it) where you creatively explore new ideas to gain insight into the problem. On the other hand, there is the “cold phase” where you iron out the details and make your ideas precise in a semi-formal way. Research requires both of these processes. And yet, it is the hot phase that excites me and where actual discovery takes place. The cold phase, on the other hand, is due diligence -- hard boring work that is necessary.

Now, just as John Harrison mentioned at one point, it would be fantastic if QED could make it easier for me to get the cold phase research over and done with. But instead, QED appears to be all about turning cold phase research into an art form all by itself. Beautiful ideas are ground out to a level of detail, formality and technicality that not only appears excessive and unintelligible (even to mathematicians) but that -- as several talks at the workshop made evident -- turn the project of formalizing a major proof into an epic undertaking, requiring quite literally man-decades of work.

The main outcome from these huge formalization projects is that a given proof is certified to be correct. For proofs of long-standing conjectures -- such as Thomas Hales’ proof of the Kepler conjecture -- this certification is worthwhile. But in my every-day work as a mathematician, correctness is not an issue. The interesting thing about a proof of a theorem in a research paper is not that it provides a certificate of correctness for a theorem. A proof is interesting when it conveys an intuitive idea for why a theorem should hold and when it reveals a new method for solving a particular type of problem. Whether the authors got all the details right is beside the point. The interesting question is whether the key idea works, and for this the human semi-formal process of mathematical reasoning suffices. Moreover, to paraphrase an argument of Michael Kohlhase, even if a proof idea turns out to be wrong: Either the idea is irrelevant anyway and then it does not matter that it is wrong. Or the idea is interesting, and then people will look at it, work with it and figure out how to get it right by way of a social process.

Publishing

The fact that formalism, technicalities and correctness are secondary becomes particularly evident when writing math papers. From my own experience I know the more technical a paper is, the less it gets looked at. By contrast, papers that convey the key ideas clearly get read, even if that entails a very informal presentation of theorems and proofs. This makes writing math papers a frustrating process, as one has to strike a fine balance between between technical correctness and conveying the intuitive ideas -- often even within a single sentence. Here, innovation in mathematical publishing could be a huge help. Separating the concerns of conveying intuitive ideas and their technical implementation -- possibly by going beyond the static PDF as the delivery format of mathematical articles -- would make life a lot easier for authors, readers and computer alike.

Computations in Proofs

Another area where computers can contribute a lot to mathematical research is carrying out large-scale case analyses and large-scale computations as part of a mathematical proof. Both the proof of the Kepler conjecture and the 4-color theorem are prime examples of this, but they are far from the only ones. Researchers at RISC routinely do such computer proofs in many different areas of mathematics. However, even as far as doing computer proofs is concerned, there seems to be a mismatch between the interests of mathematicians and those of the formal methods community. On the one hand, Thomas Hales reported at QED+20 that a major challenge in formalizing the proof of the Kepler conjecture was getting the “human proof” and “computer proof” parts to play well with each other within the formalization. Apparently, ITP systems are not tailored towards executing formally verified algorithms efficiently and accepting their computation as part of a proof. On the other hand, the mathematical community interested in computer proofs is happy to accept the computations of computer algebra systems or custom-written code as proof, even though none of these systems are formally verified! So while there certainly is interest in computer proofs, I see hardly any interest in formally verified computer proofs.

Semantic Search

As I have written previously, I view the increasing fragmentation of mathematics as a huge challenge. More and more, researchers are unaware of results in other areas of mathematics that would be relevant to their own work. This hampers scientific progress, makes research more redundant and decreases the impact of new results. Here, an efficient semantic search over a comprehensive database of known results could be a tremendous help. If researchers could simply ask a mathematical question to an automated system and be pointed to the relevant literature -- especially if the relevant literature is phrased in a vernacular of a different area of mathematics, which they may not be familiar with -- research productivity would be drastically increased.

New Ideas

Finally, there is of course the utopian hope that one days computers can discover genuinely new mathematical ideas that also provide new intuitive insight to human mathematicians. In a limited form, there are already isolated examples of such discoveries. But it seems that in general this utopian scenario is still far far away.

Flexiformality

In view of this apparent mismatch between the focus of the QED community and my own interest in the subject, I was feeling somewhat out-of-place during most of the workshop. Thus, I was very happy with Michael Kohlhase’s talk towards the end of the day.

Kohlhase argued that when comparing the number of formalized theorems and the number of math research papers published, QED is losing the race by orders of magnitude (which reminded me of a I similar remark I made some time ago). He went on to say that correctness is over-rated (mirroring my sentiment exactly) and that to be able to bring the widespread formalization of mathematics about, we need to relax what we mean by “formal”. He argued that there is a whole spectrum of “flexiformal” mathematical articles, between the informal math paper and the formal proof document in use today. Moreover, he argued that based on flexiformal articles we can achieve a whole range of objectives, such as semantic mathematical search, as long as we do not focus on certifying correctness - which is a non-issue anyway.

These comments were not only very well placed - their were also particularly delightful to me, as I had spent the afternoon brainstorming and scribbling notes (under the vague headline “zero foundations" ) on what I would expect from a useful “flexiformal” mathematical proof document.

What is a proof anyway?

I think, if we want to make any progress towards QED, then we have to radically rethink what we mean by a human-written mathematical proof document. Currently, a formal mathematical proof is taken to be a text written in a formal language with a precisely defined semantics which then is compiled -- using a fixed ITP system with a deterministic behavior -- to a low-level proof in terms of the axioms and inference rules of whatever logic the ITP is based on.

This, however, is not what a human-written proof in mathematical research paper is. A proof in a math paper has no well-defined semantics. It is not based on any clear-cut foundations of mathematics whatsoever. It is not “bound” to any fixed library of definitions and theorems or any fixed dictionary of terms. Notation and terminology is inconsistent. Citations are vague. But these are not bugs -- these are features.

The purpose of a mathematical article is not to prove a theorem, it is to convey an idea.

For this purpose, lack of any precise foundations is an essential feature of mathematical writing. The informality makes the writing far more concise and it makes the ideas stand out more clearly. It makes the content far more resilient to changes in the way definitions and theorems are stated and used in the contemporary literature (truly formal proofs "bit-rot" alarmingly fast). And it makes the content accessible to a wider range of readers from a variety of different backgrounds.

Despite all this ambiguity, I still think it is perfectly feasible to define what a mathematical article really is:

A mathematical article is an advice string intended to help the reader solve the in general undecidable problem of proving a theorem.

Most importantly, the obligation of proof lies with the reader of the article -- no matter whether the reader is a human or a computer: It is up to the reader to pick the foundations on which they want to base the proof. It is up to the reader which background knowledge they are going to use. It is up to the reader to pick the theorem that they want to prove in the first place (which may well be a different theorem than the author of the article had in mind). And in the end it is also up to the reader to decide whether the ideas contained in the article will be at all useful for the task the reader has set themselves. In particular, the advice string is in no way assumed to be trustworthy -- it does not certify anything.

This "advice string interpretation" of a mathematical article lies somewhere in the middle of the flexiformal spectrum. How such a flexiformal proof sketch might look like in detail I do not know, even though I have speculated about this before. The main objectives would be to produce an article format that is

• vastly easier for humans to read,
• vastly easier for humans to write,
• vastly more flexible in its relation to previous knowledge,
• significantly more versatile in its applicability to different problems,
• not necessarily endowed with a precise formal meaning,
• not necessarily correct, but still
• useful to computers as advice for producing proofs.

Of course such a format would be vastly more difficult for a machine to handle than today’s formal proofs. Which brings me to the last topic of the workshop.

Artificial Intelligence

Fortunately, artificial intelligence is (finally) making huge progress in QED as well. Cezary Kaliszyk and Josef Urban have done amazing work integrating existing provers with machine learning methods for premise selection and turning the whole thing into a service that people can actually use. To mention just one highlight, the hybrid system they constructed can prove automatically almost all of the individual steps that appear in today’s large libraries of declarative proofs.

This is not quite as impressive as it looks at first glance: As I found in my own experiments with declarative proofs, a large part of the work involved in formalizing an existing mathematical proof goes into choosing the intermediate steps in just the right way. Nonetheless, it is already a huge help when systems can justify individual proof steps automatically.

Of course, we still have a long ways to go before such technology could automatically interpret flexiformal proof sketches in order to produce a fully formal proof acceptable to one of today's ITP systems. And, given that I called into doubt the importance of formal correctness checks, the question arises why we should strive to have machines translate flexiformal proof sketches into low-level formal proofs at all. Perhaps Kohlhase is right, and we can achieve all the objectives that we care about without getting computers to reason at a more formal level than humans would.

However, most interesting applications, for example semantic mathematical search, arise when computers can in fact reason at a deep level about the mathematical content. Precisely because mathematicians in different areas phrase the same ideas in different language, the most interesting synergies will arise when computers can help us draw the non-obvious connections. Of course, nothing says that this reasoning has to be formal. But, in order to make sure that humans and computers do in fact talk about the same thing when reasoning about mathematics, a formal foundation certainly does seem like the most natural common ground.

Conclusion

The QED community's focus on correctness may well be a necessary first step that we need to take before we can attack the more exciting applications. However, I think the time is right to start talking about what else QED can do, especially if the QED community want to attract the attention of the wider mathematical community. I am glad that projects like MathHub.info are taking first steps in this direction, and place a particular focus on exploring new kinds of mathematical documents. No matter whether we start from an entirely formal level and build on top of that, or whether we start from an informal level and dig down: Getting working mathematicians interested in QED will require new kinds of flexiformal mathematical articles -- in between the extremes of complete formal correctness and informal prose stuck in a PDF file.

I have been positively surprised by both the quality and the quantity of events that are taking place around here. In addition to the regular Algorithmic Combinatorics Seminar and Theorema Seminar, there are always interesting workshops and conferences to go to. Mentioning just those I attended, there were:

• the workshop on Gröbner Bases, Resultants and Linear Algebra,
• the status seminar of the Doctoral Program (DK) Computational Mathematics at Strobl,
• the workshop on Computer Algebra and Polynomials as part of the special semester on applications of algebra and number theory, organized by RICAM,
• the Parallele Programming Workshop, organized by the RISC Software GmbH,
• the status seminar of our own SFB Algorithmic and Enumeratice Combinatorics at Strobl, and
• the winter school ReRiSE'14 on Reasoning Engines for Rigorous System Engineering,

in addition to several internal meetings of our SFB, both at RISC and in Vienna. Unrelated to all these local events, I was also happy to travel to Geneva to participate in the Open Knowledge Conference, back in September, which was a great experience.

Between all these goings-on and the general excitement of a transatlantic move to a new country, I also got a lot of research done. Primarily, I have been working with my good friend Zafeirakis Zafeirakopoulos on the joint project we started back in San Francisco and I have been exploring new territory with Brandt Kronholm, my fellow postdoc in the partition analysis project, and Dennis Eichhorn. In addition, I managed to finally get a couple of papers out the door which have been in the pipeline for a long time, and I have enjoyed many stimulating conversations with the people at RISC and in the SFB, leading up to exciting future projects.

Last but not least, I met a couple of very nice coders in the coworking space Quasipartikel right around the corner from my apartment. Michael Aufreiter and Oliver Buchtala are working on the fantastic editing and publishing platform Substance and I have had many in-depth discussions about Fund I/O with Martin Gamsjäger and Milan Zoufal.

All of the items above, would deserve their own blog post, but that is (obviously) not going to happen. However, judging by the experience of the last few years, the spring is always a good time to start blogging again. So, look forward to further updates soon!

Pictures

I want to close this post by sharing a couple of pictures of the beautiful scenery that comes with doing research at RISC. The institute itself is housed in the venerable Castle of Hagenberg.

The castle's tower offers a nice view of Wartberg and the valley.

My own office is in a very nice new extension building overlooking the pond.

I myself do not live in Hagenberg but the city of Linz. Here you see the view over Linz from the Pöstlingberg.

As you can see from the list above, Strobl is a favorite location for status seminars of the different working groups here at JKU. Unfortunately, these usually go from early morning to late in the evening, so that there is usually no time to enjoy the scenery. But if you can manage to squeeze in a walk between sessions and the weather plays nice, the view on the Wolfgangsee can be truly breathtaking.

"Science is based on building on, reusing and openly criticizing the published body of scientific knowledge. For science to effectively function, and for society to reap the full benefits from scientific endeavors, it is crucial that science data be made open." Panton Principles

“A piece of data or content is open if anyone is free to use, reuse, and redistribute it — subject only, at most, to the requirement to attribute and/or share-alike.” Open Definition

I could not agree more. However, what do open science and open data mean for mathematics?

As exciting as the open science and open data movements are, they appear at first glance to be largely unrelated to the world of pure mathematics, which revolves around theorems and proofs instead of experimental data. And theorems and proofs are "open" the moment they are published, right? Does this mean that mathematics is already "open"?

Of course, the word "published" is loaded in this context: The debate around open access publishing in academia is ongoing and far from settled. My personal view is that the key challenge economic: We need new funding models for open access publishing - a subject I have written a lot about recently. However, in this blog post I want to talk about something else:

What does open mathematics mean beyond math papers being freely available to anyone, under an open license?

The goal is to make mathematics more useful to everyone. This includes:

• Discovery. How can we make relevant mathematical research easier to find?
• Understanding. How can we make math papers easier to comprehend for a wider range of people?
• Exploration. How can we allow readers to interact with our work?
• Application. How can we make mathematical knowledge easier to use in many different contexts?
• Modification. How can we make it easier to build upon mathematical research?

We can open up new possibilities in each of these areas by reimagining what it means to publish mathematical research.

Mathematics as data

Examples, definitions, theorems, proofs, algorithms - these are the staples of mathematical research and constitute the main body of tangible mathematical knowledge. Traditionally we view these "items" of mathematical knowledge as prose. What if we start to view examples, definitions, theorems, proofs and algorithms as data?

Examples have always been the foundation of any mathematical theory and the discovery of new examples has been a key driver of research. As systematic search for examples (with computers and without) is becoming increasingly important in many fields, experimental mathematics have flourished in recent years. However, while many researchers publish the results of their experiments, and some great open databases exist, experimental results often remain stuck in a tarball on a personal website. Moreover, the highly structured nature of the mathematical objects encoded has led to a profusion of special purpose file formats, which makes data hard to reuse or even parse. Finally, there is a wealth of examples created with pen and paper that either are never published at all, or remain stuck in the prose of a math paper. To make example easier to discover, explore and reuse, we should:

• Create decentralized databases of examples. Think both OEIS and "github for examples".
• Promote the use standard formats to represent structured data, such as YAML or JSON.
• Acquire the parsing skills to deal with special-purpose file formats where necessary.
• Complement LaTeX papers with data sets of examples in machine readable form.
• Make uploading data sets on the arXiv common practice.
• Publish examples even if they don't make it in a paper.

The rise of experimental mathematics goes hand in hand with the rise of algorithms in pure mathematics. Even in areas that were solidly the domain of pen-and-paper mathematics, theoretical algorithms and their practical implementation play an increasingly important role. We are now in the great position where many papers could be accompanied by working code - where papers could be run instead of read. Unfortunately, few math papers actually come with working code; and even if they do the experiments presented therein are typically not reproducible (or modifiable) at the push of a button. Many important math software packages remain notoriously hard to compile and use. Moreover, a majority of mathematicians remains firmly attached to low-level languages, choosing small constant-factor improvements in speed over the usability, composability and readability afforded by higher-level languages. While Sage has done wonders to improve interoperability and usability of mathematical software, the mathematical community is still far away from having a vibrant and open ecosystem as available in statistics. (There is a reason why package managers or a corner stone of any programming language that successfully fosters a community.) In order to make papers about algorithms actually usable and to achieve the goal of reproducible research in experimental mathematics, we should:

• Publish the software we write. This includes publishing the scripts we use to run our experiments in order to make the easily reproducible.
• Write software to be used - even outside of our own office. Invest the time to polish and document code.
• Use common package repositories to publish software, not just the personal home page.
• Prefer high-level languages over low-level languages to make our libraries easier to reuse and our code easier to read and modify.
• Make software easy to install.
• Make coding part of the pure math curriculum, not just part of applied math.

Theorems and proofs are the main subject of the vast majority of pure math papers - and we do not consider them as data. However, opening up theorems and proofs to automatic processing by making their semantic content accessible to computers has vast potential. This is not just about using AI to discover new theorems a couple of decades in the future. More immediate applications (in teaching as well as research) include using computers to discover theorems in the existing literature that are relevant to the question at hand, to explore where a proof breaks when modifying assumptions, to get feedback while writing a proof about the soundness of our arguments or to verify correctness after a proof is done. The automatic and interactive theorem proving communities have made tremendous progress over the last decades, and their tools are commonly used in software verification. To be able to apply these methods in everyday mathematics, we should:

• Develop formal tools suitable for everyday use by working mathematicians (as opposed to experts in software verification or formal methods).
• Start formalizing parts of the mathematical articles we write.
• Create the infrastructure to publish and integrate formal content with prose articles.
• Explore the use of formal methods in teaching mathematics.

Mathematics for people

The points mentioned so far focus on making mathematical knowledge more accessible for computers. How can we make mathematical knowledge more usable for humans?

First of all, there is of course the issue of accessibility. From screen readers to Braille displays and beyond, there is a wealth of assistive technologies that can benefit from mathematics published in modern formats. For example, MathML provides richer information to assistive technologies than do PDF documents. Adopting modern formats and publishing technology can do a world of good here and have many positive side-effects, such as making math content more readable on mobile devices as well. But even assuming a readers are comfortably viewing math content on a desktop screen, there is a lot of room for improving the way mathematical articles are presented.

Communication depends on the audience. Math papers are generally written for other experts in the same field of mathematics, and as such, their style is usually terse and assumes familiarity with facts and conventions well-known to this core audience. However, a paper can also be useful to other readers who would prefer a different writing style: Researchers from other fields might prefer a summary that briefly lays out the main results and their context without assuming specific prior knowledge. Students would appreciate a wealth of detail in the proofs to learn the arguments a senior researcher takes for granted. Newcomers could benefit from links to relevant introductory material elsewhere. And everyone appreciates richly illustrated examples.

A single static PDF document is not the best tool for achieving all of the above objectives at the same time. By experimenting with dynamic, interactive documents, we can create articles that are more useful to a wider range of audiences. Documents could be "folded" by default, giving readers an overview first and allowing them to drill down for details where needed, possibly all the way to a formal proof. Examples could be presented side-by-side with the results they illustrate instead of the two being interleaved in a linear text. Software can enable readers to dynamically rearrange the text, for example by "pinning" definitions from the preliminaries to the screen while working through the proofs. Procedurally generated figures can be modified and explored interactively. Algorithms can be run and their execution observed - and articles could even be used as libraries from other software. Social annotation frameworks can allow readers everywhere to engage in a dialogue.

As soon as we leave the printed page behind us, the possibilities are endless. However, for these visions to fulfill their potential, openness is key. In particular:

• File formats have to be open and not proprietary. Everyone has to be able to create their own software for reading and writing these files.
• File formats have to be easily extensible, so that everyone can experiment with what a "document" can be.
• It should be possible to inspect a document to learn how it was written. (Think "show source" on a web page.) This way, authors can learn from each other by default.
• There is no reason why there should be separate software programs for "reading" and "writing" a document. The transition from "reading" to "working with" to "building on" can and should be seamless.
• Finally, licenses have to allow all of the above.

Conclusion

Open data matters for pure mathematics. Taking open principles seriously can transform mathematical research and make it more useful and relevant both within academia and in the real world.

To conclude, I want to add three more thoughts:

• Intuition is a form of mathematical knowledge that I have not mentioned so far. In my view, it is the most important one, but at the same time it is by far the most difficult one to convey in writing. The best way to communicate intuition is through dialogue. Intuitive explanations on a printed page can confuse more than they help, which is why they are often excluded from published papers. Dynamic documents can offer new room for experimenting with intuitive explanations - this cannot replace interaction in person, but which can be very valuable for anyone without access to an expert in the subject area.
• Open science and open mathematics have to be at least as much about education as they are about research. Open data that requires a team of data scientists and a compute cluster to make use of may create huge value for industrial applications, but excludes a large part of society. One of the key tenets of open knowledge is that it should be open to everyone. Being open to everyone is not just about licenses and price, however. It also means giving everyone the means to benefit from these resources. Open mathematics should empower not just experts, but learners at all levels.
• Making even a tiny fraction of these ideas happen will require a huge amount of work, and this work does not come for free. Making one math paper open means that a second paper is not going to get written. I think this is a worthy investment and creates far more value for society. However, as long as the academic job market values publication counts above everything else, this may not be a wise choice for many, career-wise. The transition to open mathematics will require both young researchers who are willing to take that risk and academic search committees who value innovation.

It is simple, really: the more people have access to an educational resource, the more can benefit from it. In an age where copying has almost zero cost and education becomes increasingly important, open textbooks and open online courses seem like the obvious way to go. However, the question how open educational resources can be funded remains unanswered.

The classical approach is to sell educational resources for profit. However, the price of textbooks is skyrocketing, instead of going down. Reasons are publishers' profit interests, market failure (professors choose textbooks, but students pay), high production costs (both for content and for printing hardcopies) and the increase in the number of students' buying used textbooks, renting textbooks and downloading unlicensed digital copies (aka "piracy") to avoid paying the full price. These trends lead to publishers pricing their textbook out of the market and are thus self-reinforcing. Clearly, the traditional business model is not sustainable.

The alternative way to fund educational resources is through donations. This can take many forms. Professors may choose to devote their time to write a book (or produce an online course) for free. Governmental agencies or private foundations may provide grant money. Companies may sponsor a course (in exchange for some form of advertising). Or a fundraising campaign could gather donations from the interested public. If donations suffice to fund an open textbook, that is great. However, except for a few high-profile examples, donations won't suffice to support high-quality educational publishing in its full breadth. (In fact, there is a theorem which, roughly, says that, if people behave rationally, the amount of money that can be raised for open content through donations is just the square root of the amount that can be raised through sales, i.e., \$1.000 instead of \$1.000.000.)

Crowdfunding is a new funding model that is working spectacularly well in the entertainment industry. While crowdfunding has yet to be tried at scale for funding open textbooks, there are two reasons why current reward-based crowdfunding models will not be a viable option for educational publishing in general. First, most successful crowdfunding projects do not promise the creation of open content. Instead, their success is critically tied to the exclusivity of rewards. Second, crowdfunding projects are typically carried by high-tier backers who pay exorbitant amounts for token rewards. While it stands to reason that the hard-core fans of an artist will happily donate large amounts of money in exchange for a casual meet-and-greet, it is hard to imagine students paying huge sums to meet their textbook authors.

Enter Fund I/O. Fund I/O is a new kind of business model that can provide access to textbooks to as many people as possible while at the same time covering the cost of production. The model is independent of donations and maximizes access instead of publisher profits. Moreover, Fund I/O provides a smooth transition towards making the textbooks open to everyone, according to a transparent mechanism.

An illustrated introduction to the Fund I/O model is given here. In a nutshell, the idea is this:

• The more students buy the textbook, the lower the price.
• As the price drops, early buyers receive a full refund for the price difference. So nobody has an incentive to wait with their purchase.
• When the price reaches a minimum value, the textbook is made free for everyone.

In particular, students (or universities, or libraries) can pledge how much they are able to pay for the content. If enough students pledge that amount, the price will drop automatically. In this way, students can determine the price of educational content.

From the publishers' point of view, the deal looks like this: Publishers limit their profits to a fixed maximum amount, right from the outset. In return, they greatly reduce their financial risks and give their customers a rational incentive to reveal how much they are truly willing to pay for the content. By giving publishers and their readers a mechanism to communicate rationally about price, Fund I/O resolves the vicious cycle of publishers charging ever more and customers finding new ways to avoid paying.

In short, whenever donations or ads do not suffice to cover costs, Fund I/O is the business model to use for funding content that serves a common good.

The prevalent business model is to provide a basic, ad-supported service for free and to charge for the full-featured service. Rates of conversion from the free to the premium service are generally low, and ads do not pay much per impression. As a result, such services are only sustainable if they reach massive scale quickly.

These economic constraints shape the software services we use - often not in a good way: Software that could run perfectly well as a standalone application is turned into a web service to funnel traffic past advertisements. Services that would work perfectly well for a small group of users are turned into yet-another social network, in order to advance scale through network effects. Companies put the interests of advertisers before the interests of their users, because advertisers are where the money comes from. User data offers additional revenue streams at the expense of user privacy. And software that caters to niche markets cannot be financed, even if the value created for its users would cover the costs of development.

Many of these constraints are not facts of life, but simply a feature of current business models. In this post I describe a radically different business model, dubbed Fund I/O for web services, that provides incentives for users to finance the development of software products and web services directly. This model is based on the Fund I/O mechanism, and provides one key feature: it gives developers and users a rational mechanism to communicate about price.

Key Benefits

Fund I/O for web services offers a number of advantages for both users and developers.

Advantages for users

• Users get access for the lowest possible price, that covers the cost of providing the service.
• Users can pledge how much they are willing to pay. If enough users pledge, the price of the service will go down.
• Early adopters receive a refund as the price goes down. Everybody pays the same price, nobody overpays.
• Users pay only for what they use. If a user ends up not using the service after they sign up, they won't pay anything.
• Users have full cost control. They never pay more than their pledge for a subscription period, no matter how much they use the service.
• By supporting developers directly, users know that the company has the economic incentives to serve their interests over the interests of advertisers or investors.

Advantages for developers

• Costs are covered through revenues. No need to finance operations through equity or debt.
• Fund I/O is optimized for growth. Prices are set automatically to maximize the number of active users, while costs are covered.
• Customers reveal how much they are willing to pay for the service, providing invaluable market data.
• Fund I/O provides incentives for price-sensitive customers to support the service financially and stop free-riding.
• Developers can focus on creating value for their customers, instead of worrying about placing advertisements or maximizing profit.

Fund I/O for web services creates a playing field that is radically different from the current model centered around VC capital, ads, freemium services and massive scale. As such, it caters primarily to web services for which the current model is not a good fit. Fund I/O is a great choice for web services that:

• do not have the scale neccessary to support itself through ads or sales of premium features,
• cannot be supported through donations alone, or
• do not have the venture capital to support years of operations at a deficit.

How it works

Fund I/O for web services is around the following three assumptions about the behavior of the majority of users with regard to web services and software:

Users want to pay as little as possible. Here, the Fund I/O model subscriptions can be of tremendous value, as it gives users rational incentives to reveal their true valuation for the product or service. This is in contrast to a classical sales context, where users would understate their true valuation and, e.g., opt for the free tier of a service, even if the value they obtain from the service exceeds the price of the premium tier.

Users do not want to buy something they do not know. Most software products and web services are not commodities. They cannot be perfectly substituted. Instead it depends on the particular characteristics of a given software product whether a user will want to work with that software at all. Thus, users avoid making a significant up-front investment without trying the product first. However, even after a trial is over, relatively few users make a purchase. In short, discontinuities in spending turn away users. A simple solution is to adopt a simple rule: Charge users in proportion to their actual usage.

Users do not want to constantly monitor their usage. Hence the popularity of flat rate offers for all kinds of services. Therefore, users should be charged in proportion to their actual usage, but only up to a fixed total amount. This way, users have peace of mind, even if they do not pay attention to how much they are using the product.

Here is an example how this could work in practice. Suppose a company wants to develop an HTML5 web app. It needs \$10,000 per month for developer salaries. To keep things simple, let us assume that on top of that, additional hosting costs are \$1 per user per month of non-stop usage. However, the average user would use the app for about 30 hours per month, which amounts to average hosting costs of about 5 cents per user per month.

The pricing now happens as follows:

• Development cost are distributed equally among all users, according to the Fund I/O for subscriptions model.
• A user counts only as a "full user" when they used the web app for 20 hours or more in the current month. A user who just tried the web app for 2 hours would just have to pay for "one tenth" of the average development costs.
• Hosting costs are passed on to the user directly. This boils down to a rate of less than 0.2 cent an hour, with an absolute maximum of \$1 per month.

Suppose the web app has a small but consistent user base of 1,000 "full" users, 500 occasional users at 10 hours per month and another 1,000 users who just stop by and look at the app for 1 hour. Then the app would have a total of 1,000 + 500 * 0.5 + 1000 * 0.05 users, which amounts to a total of 1,300 "full" users. Distributed evenly among them, the development costs amount to \$7.70 per user. So, the 1,000 full users are charged \$7.75. The 500 "half" users are charged \$3.87. And the 1,000 "window shoppers" have to pay 77 cents each. Just opening the app and looking at it for a couple of minutes would cost less than 10 cents.

Now, suppose over time the service grows by a factor of ten, so that we have 10,000 full users, 5,000 half users and 10,000 window shoppers. Then the respective price would drop to \$0.77 + \$0.05 = \$0.82 for full users, \$0.385 + \$0.02 = \$0.41 for half users and 8 cents for window shoppers. Just looking at the app for a couple of minutes would cost just 1 cent. The tremendous economies of scale inherent in web apps are passed on entirely to users. Moreover, the Fund I/O concept of average cost pricing and refunds as prices drop mean two things:

• Users can pledge how much they would be willing to pay for the service, even if their pledge is below the current price. When enough users pledge, the price will go down.
• To compensate early adopters for their investment in the service, a part of the revenues can be passed on to them as a refund for the premium they paid early on. The golden rule is that within one subscription period, everyone pay the same price for the service, no matter when they join or how much they pledge. There can also be transfers across subscription periods, for example if version 1.1 of a web service builds on version 1.0, for which early adopters paid a premium.

Of course this is not the end of the story. There are many variations that can be used to tailor this protocol to particular use cases. (See this list of posts for more details on these variations.)

• To price-discriminate low-valuation from high-valuation customers, web services can offer tiered subscriptions where the upper tiers are tied to a higher base cost. The higher tiers can include dontations made in exchange for special rewards. The lower tiers can include an ad-supported free tier; however, as a free tier decreases the incentive for users to participate in the pricing mechanism, this is not recommended.
• Producers can choose the cost function such that they make a limited profit if the service becomes popular. * Stretch goals can be used to achieve specific growth targets and provide funding for additional features.
• The fact that prices drop over time can be used to create a smooth transition to a release of the software developed under an open source license. (See here and here for more on Fund I/O for free software.)

Conclusion

Fund I/O for web services is a business model that breaks with many of the conventions we currently take for granted in the internet economy. At the heart of the model is a transparent mechanism for users and developers to communicate rationally about price. Users actively shape the pricing of the web service through the very payments they make. Developers cover their development costs while reducing their dependence on advertisers and venture capital. Fund I/O for web services makes web services for niche audiences sustainable and at the same time provides them with a smooth transition to serving mass audiences if they become popular. Finally, Fund I/O offers a flexible toolbox that can be adapted to many different use cases.

Fund I/O offers a felxible toolbox of concepts for designing innovative business model, and it is just the beginning: There is plenty of room for disrupting the internet economy.

A variant of Fund I/O that finances ongoing fixed costs is the following subscription model. Of course, each particular use-case will require further tweaks, but the basic model is this.

• Each period creates new fixed costs. A period can be a time interval or a new release. An example would be \$5,000 every month.
• Each customer submits a pledge for how much they would be willing to pay each period for access to the subscription. Let's assume that on June 1st there are 100 people who submitted a pledge of \$50 or more, and a few more who pledged less than \$20.
• The price is chosen as low as possible such that the costs are covered. Costs are distributed evenly among all subscribers who get access. In the example, the price would be set \$50 and the 100 people who pledged at least as much receive access for the current month of June.
• As more subscribers sign up the costs drop. Say, another 100 people pledge at least \$25 by June 5th, then the price drops to \$25 and these 100 people receive access to the subscription for the month of June.
• Previous subscribers are refunded the price difference. Each of the original 100 subscribers receive \$25. This can either be a cash refund or a credit that can be applied to the next months' subscription fees.
• Pledges remain active across periods. So if nobody changes their pledge, the subscription will cost exactly the same amount every month.

Just as in the case of one-off payments, the Fund I/O model has a number of advantages over classic subscription models.

• Customers have an incentive to reveal their true valuation for the product.
• The subscription is provided at the lowest possible price to the largest possible audience, while costs are covered.
• Customers determine the price of the subscription through a transparent mechanism.

The subscription model described above can serve as a foundation for many different variants.

• Rolling subscriptions can be incorporated into the pricing scheme. One customer can subscribe for June 1st till July 1st while another subscribes from June 5th till July 5th.
• "Stretch-goals" can allow customers to determine the scope of the subscription through their pledges. If pledges are high enough to provide \$10,000 per month, another staff member can be hired, for example.
• Periods can build on each other. Subscribers to version 1.0 of a software package can get refunds from sales of version 1.1, as the development work put into 1.0 clearly benefits 1.1.
• And, of course, a share of the revenues can go to the producers as profit beyond the fixed costs for each month. These profits can serve as capital to provide funding for months with insufficient subscriptions.

Bottom line: Fund I/O is well-suited to subscription services. In the next post, I will go into detail on how this can be used to fund web services.

Fund I/O can be used not only for digital goods, but for anything that has large fixed costs and low marginal costs. This includes physical goods that have a large social impact, such as vaccines. Here is how this might work.

Suppose a vaccine for a certain disease has already been developed. Now it needs to be produced at scale to reach millions of people world wide. The problem is vaccine production requires a substantial investment to get going. This means, if a supplier were to produce just 100,000 doses of the vaccine, each dose might be prohibitively expensive. But at a scale of 10 million doses, each dose could be very cheap. As long as the market is small, the price for the vaccine will be very high so that only few people will be able to afford it. But once the market grows, the price will drop, and many more people will be able to afford the vaccine.

This creates a chicken and egg problem: To get the price down, many people would need to buy the vaccine. But for many people to buy the vaccine, the price would need to drop. So how can we get the market started?

One approach to getting the market started are advance market commitments. A couple of large buyers of the vaccine, such as governments or charitable donors, make a joint commitment to buying a large number of doses at a specified price. The idea is that by guaranteeing a certain demand for the vaccine in advance, the market can be jump-started at a volume attractive to suppliers and at a price attractive to buyers.

There is a catch, however: Because, the price for the vaccine will drop over time, buyers have an incentive to wait. Those who start buying early will pay a premium. It you wait, you pay less, and the later you get in, the more you save. Even if everyone wants to buy the vaccine, those who manage to start buying last will pay the least. Early adopters effectively subsidize late entrants.

You can imagine that this leads to quite a lot of maneuvering over who gets to be the last. Especially because the market for governments buying vaccines has several features that exacerbate the problem: First, very large sums of money are at stake. Second, buyers (such a governments) are often frugal, by necessity. Third, implicitly subsidizing other parties may be unpopular, even if it is for a good cause such as getting more vaccines to more people. And finally, the only benefits of entering early are measured in terms of impact (saving lives) and not profit (return on investment), which often makes spending money harder instead of easier - unfortunately. Advance market commitments can help a lot in this setting: by forming a coalition of first movers, the financial disadvantage to buying early is reduced considerably. But the incentive to get in later remains, and this makes it often very hard to establish such a coalition.

Here Fund I/O can help. In fact, Fund I/O was designed to solve exactly this chicken-and-egg problem. Using Fund I/O, buyers do not have an incentive to wait. To achieve this, all you need to do is apply the refund mechanism used in the second phase of the Fund I/O model. Buyers can purchase immediately and still benefit from economies of scale as the market matures. Through the refund mechanism, they can rest assured they will benefit from decreasing prices in just the same way as a late entrant.

This solution makes jump-starting markets much easier, by offering a smooth transition from a low volume/high price market to a high volume/low price market. Moreover, it does not require complicated negotiations aimed at getting buyers to commit to making purchases now, even though it would be in their financial interest to wait. The Fund I/O mechanism guarantees the same financial benefits as an advance market commitment involving all potential buyers, present and future, but it can be set in motion by just a few interested parties right away. Agreements are not made at a negotiating table but on a platform of exchange that incentivises all participants to reveal their true valuation for the vaccine.

Of course there are many more details to be addressed here, both as far as the theoretical model and practical issues are concerned. But these general considerations already make clear the Fund I/O shines at resolving difficult negotiations of this type by intermediating price differences across time.

Why Funding Open Source Software is Difficult on Kickstarter

Crowdfunding has taken off, for physical goods as well as for software-related products like games. So why do we see so few open source project take advantage of crowdfunding? In fact, Kickstarter is based on the Street Performer Protocol (SPP), a method for raising funds that was originally intended as a model for financing open source software, and that had some early successes such as making Blender open source. Could it be that rewards-based crowdfunding as on Kickstarter simply does not work as well for open source software?

There is one subtle difference between open source and closed source projects on Kickstarter, and this difference may be crucial: The successful game projects on Kickstarter have no intention of giving away their core product for free. This makes pledges pre-sales instead of donations. Open source projects on the other hand announce right away that their product is going to be free. Does this influence backer behavior?

It is certainly true that many crowdfunding campaigns are successful because some altruistic backers pledge huge amounts of money to the project - much more than they would need to pledge to get a copy of the product for themselves. But projects rarely can be funded through such altruistic contributions alone. Take a look at Shrouds of the Avatar, for example: the large majority of backers pledged the minimum amount required to receive a copy of the game. These backers are obviously price conscious and don't pledge more than they have to. I will call these backers rational, in the economic sense. This means that they are self-interested and act to maximize their own welfare.

This leads me to the following working hypothesis:

Crowdfunding projects need contributions from both rational and altruistic backers to raise large amounts of money.

This would explain why open source projects appear (so far) to be less successful than other creative projects at raising money via crowdfunding: Because open source software is (going to be) free, rational backers don't pledge anything.

In fact, there is research in the economics literature on the optimal behavior of an entirely rational backer who is faced with the decision of backing an open source project. The amount he or she is willing to pledge is determined by the probability of their pledge being pivotal and getting the project funded. Backers correctly observe that this probability decreases with the total number of backers interested in a project. A consequence is that - if all backers were rational - the amount of money open source projects can expect to raise grows only proportional to the square root of the number of people interested in the project. In contrast, the amount a closed source project can raise grows linearly in the number of people interested in the project. This can quickly lead to a difference of several orders of magnitude!

(Now, before anyone gets a wrong impression: I do not think that people behave entirely rationally or that they should behave rationally. It is vital for our society that people act out of altruistic motives. And it is great that crowdfunding has found a way to get altruism to scale, so that we can make great things happen. I think we should look for more ways in which we can integrate altruism into our economic activities. All I am saying is that there is a reason that our entire economic system is built on the assumption that people tend to behave rationally. Our goal should be to find economic models that incorporate both altruistic and rational motives.)

Fund I/O as a Model for Funding Open Source Software

Fund I/O is a new crowdfunding model based on the Average Cost Threshold Protocol (ACTP). (If you are not yet familiar with Fund I/O, you may want to check out this example before continuing here.) When I developed the ACTP, one of my goals was to find a crowdfunding model that would work for open source software. And in many ways Fund I/O achieves precisely that:

• Most importantly, Fund I/O gets rational backers to reveal how much they would truly be willing to pay for the software.
• This allows open source project to raise as much money as closed source projects.
• Moreover a project can raise more money on Fund I/O than using the Kickstarter model, because it lets the market determine the optimal price of the product.
• At the same time, Fund I/O still allows altruistic backers to dontate as much as they want to the project. (This requires Fund I/O to be used with the option of allowing each backer to set their own minimum price level.)
• Finally, Fund I/O provides a clear path towards the relase of the software product under an open source license.

Now, you may have noticed that I did not quite say Fund I/O "works" for open source software. In fact, I do not think the Fund I/O model gives me everything I would personally want from an open source funding model. However, I do think it works much better than anything that is currently out there. So let me first explain in what way it does work for open source software. In the next section I will then go on to explain the limitations I see.

Fund I/O works great for open source projects if your project meets the following assumptions:

• Your goal is to finance the creation of version 1.0 - no more.
• You are willing to release your software under a closed license at first.

Then you just run through the three phases of the Fund I/O mechanism (with individual minimal price levels) and at the end:

• you have completed the software you wanted to write,
• you have released the software and its source code under an open source license, free for everyone to use and modify,
• your costs were covered right from the start and
• you even made a certain profit that you can determine in advance.

The release under an open source license happens if and only if there is enough altruism among your customers to finance the costs of production through voluntary donations. However, this absolutely not the same as simply using the SPP. First of all, your project gets made if there is enough rational interest in your software. It just won't be open sourced unless there is enough altruistic interest. Second, Fund I/O achieves a smooth transition from the state where there are few users who would need to donate very large amounts to the state where there are many users who need to donate just a couple of dollars. This lessens the burden on any individual donor considerably. Moreover, the donation is a sunk cost for the customer: donating means forgoing future refunds instead of paying money now. All of these factors make it much easier to gather the required donations, than using the SPP, even if Fund I/O is used with individual minimal price levels. If a fixed minimal price level is used for everyone, then gathering the required donations gets easier still.

Caveats

Now, I believe the above could work great for developing, say, an open source game. But for open source software I see a couple of caveats.

First of all, the user base of the software has to be willing to use closed source software during the second phase of the protocol. If a substantial number of users will never run anything but free software, then you are of course out of luck. I do not think this will be a problem; it was not a problem for Light Table during its crowdfunding campaign.

Second, it has to be reasonable to make the software non-free during the second phase. This means that the software is for sale and according to the license users are not allowed to pass copies of the software along to their friends. This is a stronger restriction than just not releasing the source code and may turn off more of the free software crowd. More importantly, this limits viral marketing effects during the crowdfunding and sales phases. People have to buy the product to try it out. (Even though a demo could certainly be offered.)

Of course the whole point of Fund I/O is that because of the refund mechanism, there is less of a disincentive to buying than in a classical sales context. In particular, if a customer sets their minimal price level to zero, then they get a full refund in case the software is released as open source. But in a world where many people expect application software (as opposed to games) to be free, this may be a hurdle. I'd be optimistic and say that the compromise of making software non-free for a limited amount of time, according to a transparent mechanism, in order to cover the costs of development is convincing enough to assuage these concerns.

Finally, and most importantly from my point of view, software requires maintenance. Application software needs to be developed continually. A game may be "done" after the 7th patch or so, but application software never is. If the only goal is to fund the creation of a version 1.0, then this is not a problem. But what if you are looking for a way to finance the development of open source software throughout its entire lifecycle?

An obvious modification to Fund I/O for financing several consecutive versions would be to run a new campaign for each major version. The mechanism could easily be adjusted to make a part of the revenues from the version 2.0 sales refunds for version 1.0. And once 1.0 is free, buyers/backers of subsequent versions could stop paying refunds to version 1.0 owners. The problems I see with this are therefore not theoretical, but practical in nature. The company developing the software would have to maintain several versions of the software side-by-side, they would have to backport security patches and provide support, and they would have to finance these activities from their version 2.0 revenues. While all of these concerns appear in commercial (and open source) software development anyway, they are exacerbated by keeping different versions under different licenses around - just because of the funding scheme.

Ultimately, it will depend on the particular project which of these considerations are relevant, and which variant of Fund I/O makes the best fit. Personally, I view Fund I/O as a toolbox that can be tailored to fit many different needs.

Conclusion

I hope to have convinced you that crowdfunding open source software is possible at much bigger scale than we have seen so far. What we have to do to make this happen is to find a crowdfunding model that takes the backers' diverse patterns of economic behavior into account. I think Fund I/O is a step in the right direction, but can certainly be improved upon with regard to funding open source software.

What do you think would be the challenges when applying Fund I/O to open source software? How would you modify Fund I/O to make it more applicable to open source software? Comments and questions are welcome!

What is the Fund I/O business model? Fund I/O is a business model for the production of goods with substantial economies of scale. In a nutshell:

• Financing is provided through presales made during a crowdfunding campaign.
• The producer commits in advance to a pricing scheme that passes savings due to economies of scale on to customers directly, by lowering prices as fast as possible.
• Early buyers are guaranteed to get a refund when the price drops, so that they have no incentive to wait with their purchase.

If you are looking for details, good places to start are fund-io.com and this example.

What makes Fund I/O different from the conventional way of doing business? Suppose you run a company and want to produce a product that benefits from economies of scale. Here is what Fund I/O means to you:

• You finance your product entirely through presales. You do not have take on a loan, you do not have to pay interest, and you do not have to maximize profit for your investors. This drastically reduces your risk and your cost of capital. The presales appear as a non-interest bearing liability on your balance sheet, and the primary interest of your financiers is to receive a great product, not to get paid.
• You place an absolute limit on the profit you can make off a product. This limit can be chosen arbitrarily, but by choosing a refund scheme you are committing to an absolute limit on your profits. Note that because you used presales from customers to finance production you are making a profit without having invested any capital yourself, so from that point of view your return on investment is infinite, even if your maximum profits are not!
• You obtain a tremendous amount of market information: By committing to a refund scheme, you give your customers an incentive to reveal exactly how much they are willing to pay for your product. This translates into higher sales, more revenue and faster growth.

Through the combination of crowdfunding, a clear price reduction scheme with a limit on profits and a refund mechanism, Fund I/O manages to align the interests of key stakeholders and it provides them with a mechnism to communicate truthfully about value: It resolves the fundamental conflict of interest between investors who want to maximize their profits and customers who want to minimize what they have to pay.

What makes Fund I/O different from other crowdfunding schemes? There are basically two different crowdfunding models out there: reward-based crowdfunding and equity crowdfunding.

Equity crowdfunding is not that different from the conventional business model. Financiers are still interested in return on investment. The key difference is that investors often have another stake in the business in addition to their profit interests. For example, they may be not only investors but customers at the same time, or they may have an interest in the social impact of the business. But still the business is obliged to maximize profits on behalf of its investors, which gives customers incentives to understate their valuation of the products the business is offering.

Reward-based crowdfunding makes customers the financiers of a product, aligning the interests of two key stakeholders. But it still does not provide a mechanism to communicate about value. In reward-based crowdfunding, creators have to fix the price a priori and often a majority of backers pledge just this price and no more. The success of reward-based crowdfunding hinges on the generosity of backers who self-select for price targeting by willingly paying a large premium for the product. This type of altruism (whether motivated by appreciation of the project, the thrill of being part of something great or the enjoyment of receiving secondary merchandise) is great, if it suffices to finance the project. Fund I/O can be tweaked to captialize on this type of gift economy as well, but the main contribution of Fund I/O lies elsewhere: Fund I/O makes crowdfunding work in cases where the capital requirements of a project are large or where the potential customers are price sensitive. Fund I/O provides the mechanism that allows producers and customers to join forces in order to create great products, even if all parties involved need to avoid paying more than they have to.

What problem does Fund I/O solve? From the point of view of a business, Fund I/O reduces risk, aligns interests of stakeholders, provides a wealth of market information and generates more sales. Moreover Fund I/O provides financing alternatives to debt and equity and conventional crowdfunding. This is particularly useful in cases where debt and equity are too expensive, too risky or simply unavailable and when altruistic contributions made through a rewards-based crowdfunding campaign do not suffice.

However, this is just one angle on the question: "What problem does Fund I/O solve?" Over the next days, I will post other answers, taking the point of view of a customer, or examining the applicability of Fund I/O to non-profit projects aimed at social impact. One very technical answer is already written up: Fund I/O provides a practical implementation of an incentive compatible, individually rational mechanism for the private provision of excludable public goods that is asymptotically optimal.

As you may have seen, I have been blogging recently about a new crowdfunding mechanism for public goods, the Average Cost Threshold Protocol. Since the last post on the topic, I have spent quite some time discussing this idea with people, and have decided to give this idea into a project dubbed Fund I/O with an own website fund-io.com and an own Twitter account.

To get updates about his project and idea, you can subscribe to a (very-low volume) mailing list on the project website, or just follow this blog. I'll keep posting whatever I have to say on the subject of fair crowdfunding on this blog. (If and when Fund I/O gets its own blog, I will make an announcement here.)

Finally, in case you are wondering, Fund I/O is not a startup. (Not yet, anyway.) The current goal of Fund I/O is to try some variant of the ACTP in practice. If you have got just the right project in need of a revolutionary funding mechansim, let me know!

[Note: I am using Sage Cells to produce the pictures in this post. This has the advantage that you, dear reader, can interact with the pictures by modifying the Sage code. However, this will probably not run everywhere. It certainly won't work in most RSS readers...]

Here is the graph of the GCD! First a little static preview...

... and now a proper interactive graph. Be sure to rotate the image to get a 3d impression. (Requires Java...)

What precisely are we seeing here? The gcd is a function $\mathrm{gcd}:\mathbb{N}^2\rightarrow\mathbb{N}$. Its graph is a (countable) set of points in $\mathbb{N}^3$. This graph is precisely the set of integer points contained in one of the (countably many) lines indicated in the above picture. The value of the gcd is given by the vertical axis.

Now, what are those lines? Suppose $a$ and $b$ are two natural numbers that are relatively prime, i.e., $\gcd(a,b)=1$. Then we know that $\gcd(ka,kb)=k$ for any positive integer $k$. So all (positive) integer points on the line through the origin and $(a,b,1)$ are in the graph of the gcd. Conversely, for any numbers $x,y$ with $gcd(x,y)=z$, we know that $\gcd(\frac{x}{z},\frac{y}{z})=1$, that is, the point $(x,y,z)$ lies on the line through the origin and $(\frac{x}{z},\frac{y}{z},1)$. So by drawing all these lines, we can be sure we hit all the integer points in the graph of the gcd.

What I find very beautiful about this is that when looking at this picture from the right angle, you can see the binary tree structure of this set of lines. It is precisely this binary tree that we walk along when running the Euclidean algorithm. The lines in the above picture are color coded by their depth in this "Euclidean" binary tree.

The version of the Euclidean algorithm I like best this one. Suppose you want to find $\gcd(a,b)=1$. If $a>b$, compute $\gcd(a-b,b)$. If $a<b$, compute $\gcd(a,b-a)$. If $a=b$, we are done and the number $a=b$ is the gcd. At each point in the algorithm we make a choice, depending on whether $a>b$ or $a<b$. If we keep track of these choices by writing down a 1 in the former case and a 0 in the latter, then, for any pair (a,b), we get a word of 0s and 1s that describes a path through a binary tree. As we walk from one pair $(a,b)$ to the next in this fashion, we trace out a path in the plane: For each 1 we take a horizontal step and for each 0 we take a vertical step. This path can look as follows.

Now comes the twist. We can turn the Euclidean algorithm upside down. Instead of walking from the point $(a,b)$ to a point of the form $(g,g)$ and thus finding the gcd, we can also start from the point $(1,1)$ and walk to a point of the form $(\frac{a}{g},\frac{b}{g})$ to find the gcd $g$. (Why $(\frac{a}{g},\frac{b}{g})$? Well, $(\frac{a}{g},\frac{b}{g})$ is the primitive lattice vector in the direction of $(a,b)$. In terms of the graph at the top, $(\frac{a}{g},\frac{b}{g},1)$ is the starting point of the ray through $(a,b,\gcd(a,b))$.)

How do we get there? We start out by fixing the lattice basis with "left" basis vector $(0,1)$ and "right" basis vector $(1,0)$. Their sum $(1,1)$, which I call the "center", is a primitive lattice vector. Now we ask ourselves: is the point $(a,b)$ to the left or to the right of the line through the center? If it is to the left of that line, we continue with the basis $(0,1)$ and $(1,1)$. If it is to the right of that line, we continue with the basis $(1,1)$ and $(1,0)$ and recurse: We take the sum of our two new basis vectors as the new center and ask if $(a,b)$ lies to the left or to the right of the line through the center, and continue accordingly. If $(a,b)$ lies on the line through the center, we are done: the gcd of $a$ and $b$ is the factor by which I have to multiply the center to get to $(a,b)$.

As we follow this algorithm, we draw the path from one center to the next, until we reach $(\frac{a}{g},\frac{b}{g})$. Then we get the following picture. It looks almost like a straight line from $(1,1)$ to our goal, but it is only straight whenever we take two consecutive left turns or two consecutive right turns. Whenever we alternate between right and left, we have a proper angle, it only gets difficult to see this angle the farther out we get. If we write down a sequence of 1s and 0s, corresponding to the left and right turns we take, we get the exact same sequence as with the standard Euclidean algorithm.

The obvious next step is to draw the complete binary trees given by the above two visualizations of the Euclidean algorithm (up to a certain maximum depth). Drawing the first tree gives a big mess, because many of the edges of the tree overlap. You can clean up the picture by removing the lines and drawing only the points: In the code below comment the first definition of thisdrawing and uncomment the second. This then gives you a picture of all primitive lattice points (pairs of relatively prime numbers) in the plane at depth at most maxdepth in the tree.

The second variant of the Euclidean algorithm gives a much nicer picture, revealing the fractal nature of the set of primitive lattice points. The nodes of the tree, i.e., the points drawn in the picture are the starting points of the rays plotted in the 3d graph of the gcd given at the beginning of this post. In this way, this drawing of the tree gives the precise structure of the binary tree intuitively visible in the three-dimensional graph. One thing you may want to try is to increase the maxdepth of the tree to 10. (Warning: this may take much longer to render!) Note how far out from the origin some of the points at depths 10 are.

The reader may have observed that the binary tree described in this post gives us a very nice way of enumerating the rational numbers. Calkin and Wilf made this observation in the paper Recounting the Rationals, whence it is sometimes called the Calkin-Wilf tree, even though Euclid tree might be a better name as it is given by the Euclidean algorithm itself. As we have seen above, a look through the lens of lattice geometry tells us how to draw this tree in the plane and how to find it in the graph of the GCD.

Does the Average Cost Threshold Protocol incentivize content creators to "sue the Internet"?

Very short answer: The incentive for creators to sue the Internet is very small (much smaller than usual) but not zero.

Short answer: The Average Cost Threshold Protocol (ACTP) drastically reduces the incentive of content creators to sue people, as creators' costs are covered from the start. Moreover it drastically reduces the incentive for people to copy content outside of what is allowed by the protocol, because buyer's payments are used to lower the price (for themselves and others) and to eventually release the content under a copyleft license.

That said, there is a "sales phase" in the protocol where such incentives exist, even if they are limited. However, this drawback is outweighed by the protocol's key advantages:

• Creators can expect to raise significantly more money than with funding models that employ only copyleft licenses.
• Creators and users agree from the outset on a clear path towards release of the content under a copyleft license.

Moreover the protocol can be modified so that creators have no incentive whatsoever to sue the Internet - however, in this case creators also lack an economic incentive to deliver a great product.

Long answer: Here are the key reasons why creators have very little incentive to sue the internet, if they choose to adopt the ACTP.

• The protocol guarantees that creators' costs are covered before content is ever released. This drastically reduces the creators' financial risk, which in turn reduces the threat unlicensed copies pose to creators.
• Costs are covered by users, not investors. This frees creators from having to worry about paying back loans or maximizing their return on equity. Thus the creators' economic goal is to maximize user value not shareholder value.
• The ACTP provides a clear path towards releasing the content under a copyleft license. By adopting the ACTP, creators subscribe willingly to this goal.
• Creators' profits are maximized if and only if the content is released under a copyleft license, at the end of ACTP. This means that creators' have an incentive to work towards the goal of releasing the content for free.

That being said, the ACTP does have a "sales phase" where the content is available only under a "closed" copyright license and people have to buy access. In this sales phase, users have an economic incentive to obtain unlicensed copies.

• Creators receive a share of the revenues earned during the sales phase as profit. They thus have an incentive to sue people who avoid paying for access in the sales phase.
• However, if there are enough buyers to "free" the content and cause its release under a copyleft license, then the creators do not care how many people made unlicensed copied during the sales phase: their profits in this case are fixed from the start.
• The ACTP could be modified so that creators do not receive any profits during the sales phase. All revenues from sales could go towards lowering the price by refunding previous buyers/backers. In this case creators do not have any incentive whatsoever to sue the Internet, at any point in time. However, I do not think that this is a good idea. Because in this case, creators' do not receive any revenue after the initial fundraising campaign and thus they have no economic incentive to make their product shine and promote it accordingly.

Moreover, the ACTP provides incentives for users to actively participate in the sales phase of the protocol by paying, instead of by making or obtaining unlicensed copies:

• In the short term, the more people pay, the faster the price will drop. As a buyer this means you yourself will get a larger refund and at the same time you will enable other people to afford access.
• In the long run, the more people pay, the sooner will the content be released freely, under a copyleft license.

The sales phase thus becomes a cooperative game among users, where they can help each other by lowering the price in the short term and ultimately "freeing" the content for everyone. This of course has the drawback that it might cause cooperative users (who buy) to sue uncooperative users (who make or obtain unlicensed copies). But the amount of refund money cooperative users stand to loose from unlicensed copies is very limited, so I hope this is not going to be an issue. Users who obtain unlicensed copies hurt themselves by making it less likely that the content is eventually going to be officially released under a copyleft license.

But why should we have a "sales phase" at all? Would it not be better to release the content under a copyleft license right away? The reason is a phenomenon that has been well-studied in the economics literature: By restricting access to content during the sales phase, it is possible to raise significantly larger amounts of funds for the creation of digital content than would otherwise be possible. In economics jargon: It is significantly easier to raise funds for the private provision of a public good with use exclusions than for the private provision of a pure public good without use exclusions. The amount of money we can raise for content that is going to published under a copyleft license from the start grows on the order of $\sqrt{n}$ where $n$ is the number of people in the economy. If we introduce use exclusions, on the other hand, the amount of money grows on the order of $n$. This is a difference of several orders of magnitude, with a huge potential impact in practice! (I will write more about these results in a future post. In the meantime I recommend this post and these two articles.) The ACTP aims to strike a balance between the conflicting goals of publishing free content and raising funds by employing use exclusions in an intermediate phase and providing a clear path towards release under a copyleft license.

Bottom-line: The ACTP does a far better job of aligning incentives than any other mechanism for funding digital content that I know. I think it goes a long way towards resolving the economic conflict over copyright and I can't wait to put it into practice and try it out.

The reason is a conflict of economic interests. On the one hand we need to fund the creation of digital goods. On the other hand, our creation can do the most good if it is made available to literally everyone. But how can we convince people to pay for a digital good, if they know that eventually everybody can download a copy for free? What we need is a new idea that addresses both of these issues: the public welfare and the profitability of creating digital goods.

In this regard crowdfunding platforms are very promising, as they can in principle be used to fund digital goods that are then made freely available to everybody. However, a closer look reveals that in practice the digital goods financed by crowdfunding campaigns are often sold like apples - as if they could not be copied at all. Here is one idea how we can do better:

The Average Cost Threshold Protocol is a fair crowdfunding mechanism that takes economic interests of both users and creators into account.

How it works is best explained by way of a concrete example. Suppose a company wants to raise \$1,000,000 to finance the production of a computer game. They start a crowdfunding campaign on a website implementing the Average Cost Threshold Protocol. The website starts collecting pledges until a deadline is reached. Suppose on the day of the deadline the pledge look as in picture below. In particular, we find that there are 20,000 people who pledged \$50 each or more. If all of them pay exactly \$50, then the company's costs will be covered and everybody will have paid the same amount. Moreover \$50 is the lowest price that covers costs: for example 24,000 people would be willing to pay \$40, but that yields only \$960,000. This lowest price now becomes the threshold price: everybody who pledged at least \$50 pays exactly \$50 and they become backers, who will receive a copy of the game once it is finished. All others do not pay anything and do not get a copy. The principle is simple: the costs of production are distributed equally among all those who get access. The threshold price is chosen such that it provides access to the largest number of people at the lowest possible price such that the costs of production are covered.

Now that the game is released, more people have heard about it and want to purchase access. Typically, the company would simply sell copies and keep the revenues as profit. But here comes the twist! Instead of paying a fixed price, interested buyers submit pledges on what they would be willing to pay for the game. Suppose there are another 10,000 people who each pledge \$40 or more. Then we drop the price to \$40 dollars and charge each newcomer \$40 for a copy of the game. The revenues of \$400,000 are split 50-50. One half goes as profit to the company. The other half goes to the original backers, who each get a refund of \$10. Following this principle the price keeps dropping the more people buy the game and thanks to the refunds everybody who gets access is guaranteed to pay the same price no matter how much they pledge or when they pledge.

The more people buy the game, the lower the price for everyone. And the lower the price, the more people can afford to buy the game! What if this virtuous cycle takes off and the game becomes really popular? At this point another feature of the mechanism kicks in: At the very beginning of the crowdfunding campaign a price of freedom of \$10 is announced. This means that as soon as the threshold price drops to the price of freedom of \$10, the game is made available to everyone, the whole world, no matter if they paid or not. This includes the release of the game under a copyleft license as well as the publication of all source code and assets, to allow people to freely modify the game. In the example, the price of freedom of \$10 is reached if the game becomes so popular that at least 180,000 people buy the game. In this scenario, the company has not only covered its costs, but on top of that it also made a profit of \$800,000. (This amounts to an infinite (!) return on investment as the customers contributed all the funding for the project!) The public gains a game they are free to use and modify. And the backers and buyers of the project spent only \$10 each, both to gain early access to the game and to make all of this happen.

We can even go one step further and allow every customer to set their own price of freedom, that is, the price below which they do not care to receive refunds. With this small modification, it is entirely rational for people to pledge exactly as much as they are really willing to pay for the game. This is a truly amazing property that most other methods of raising funds do not satisfy. In a retail sales context, on Kickstarter, in you-name-your-price mechanisms like the Humble Bundle, customers always have an incentive to understate how much the product is worth to them. Here, even entirely self-interested customers have an incentive to tell the truth, at every point during the process. This is not the end of the story, though! The Average Cost Threshold Protocol has a host of variations and wonderful theoretical properties.

As you can see, there is a lot of room to improve upon existing methods for funding digital goods. In a world where digital goods make up an ever increasing percentage of the global economic output this can have a profound impact on our economic lives. With new ideas and experiments we can come up with business models that can raise large amounts of money to finance the creation of high-quality digital goods and at the same time make sure that as many people as possible get access. In particular, we can provide a clear path towards releasing digital goods under a copyleft license. This way, everybody can benefit from the economic power of copying!

If you like that sort of thing, check out this video or these lecture notes.

In this post, I want to describe a different way to fund the private provision of public goods: the Average Cost Threshold Protocol.

Before we get started, let me clarify what I mean by the term public good. The term does not have the egalitarian meaning of a common good that is shared by everyone and that all members of a community are entitled to. Rather, a public good is any good that has a specific economic property: If a public good is provided to one person, it could also be provided to everybody else at no additional cost. Note that I am not saying the public good actually is provided to everyone. It may very well be that some people are excluded from using the public good. Also, I am not saying that nobody has to pay anything for the public good.

Practically all digital goods are natural public goods. This includes movies, music, ebooks, online lectures, scientific articles, software and computer games. These can, in principle, be copied at virtually no cost. Often, legal or technical restrictions are placed on copying these goods, as producers want to raise money for the provision of these goods by selling these goods as private goods (or by selling advertising tied to these goods). This post is about finding better ways to fund the creation of such digital goods. As my running example of a public good, I am going to use a computer game. Not because games are the most important type of public good, but simply because they are widely popular, require no maintenance after their release (or after, say, the tenth patch) and because a number of computer games have been very successful on Kickstarter, which shows that the audience is open to experimenting with new funding mechanisms.

The Theory of Average Cost Pricing of Public Goods

A very natural variation of threshold pledge systems like the Street Performer Protocol is a fixed fee mechanism with average cost prices. In this section I will present the theory behind this mechanism, before turning to its practical implementation (and a practical example!) in the next section.

The basic idea is very straightforward:

1. Everybody interested in a given project makes a pledge, saying they are willing to contribute a certain amount of money to funding the project. If somebody is not interested in contributing that just don't pledge anything.
2. After all pledges have been made, we distribute the costs of the project equally among as many people as possible: Everybody pays exactly the average cost of the project, as long as they pledged at least as much. More precisely, we figure out the smallest price $p$ such that if everybody who pledged at least $p$ pays exactly the price $p$, then the costs of the project are covered exactly. Nobody pays more than $p$ and if somebody pledged less than $p$ they don't have to pay anything.
3. If there is no such price $p$, for example because people pledged too little, then the project is not funded and nobody pays anything!
4. In case the project is funded, the money raised is used to create the public good. But only those people who paid get access to the public good! (Here we assume that the public good in question is excludable.)

Points 1 and 3 are very similar to the Street Performer Protocol (SPP) and what happens on Kickstarter. Point 2 is crucially different, as in the SPP and on Kickstarter everybody pays what they pledged and not the price $p$. Point 4 is what happens in many projects on Kickstarter, as I observed in my last post, but it is very different from the idea behind the SPP, which was intended to fund pure public goods without use exclusions. There is another vital difference to what happens on Kickstarter that will become clear in the next section.

The fixed fee mechanism with average cost prices has crucial theoretic advantages:

• Everybody has an incentive to pledge exactly what the project is actually worth to them. The technical term for this incentive compatibility. Note that the SPP is not incentive compatible: there, people have an incentive to understate the value the project has for them, in order to pay less. (This is called "free riding" in the public goods literature.)
• Nobody is forced to contribute anything if they don't want to. In other words, no matter what happens, after we have used this mechanism, everybody will be at least as well-off as before. This is called individual rationality. Many mechanisms for funding public goods, both practical ones, such as taxation by the government, and theoretical ones, such as the Groves-Clarke mechanism, are not individually rational. But for the private provision of public goods in which people participate voluntarily, individual rationality is essential.
• If the fundraising is successful, we raise exactly as much money as is needed to fund the project. That is, the mechanism not only covers costs but moreover it balances the budget.

Of course this mechanism also has a key disadvantage: We exclude people form using the public good even though the public good could be provided to them at no extra cost. In technical terms we say the mechanism is inefficient. This, however, is unavoidable as there are theoretical results such as the Myerson-Satterthwaite Theorem which says, roughly, that there does not exist a mechanism for the provision of public goods that is incentive compatible, individually rational and efficient. This result tells us that the first best solution of giving everybody access to the public is impossible to attain. The good news is, though, that in face this impossibility result, the fixed fee mechanism with average cost prices is the best possible alternative:

• According to a result by Peter Norman the above mechanism is (asymptotically, in a large economy) the most efficient one among all mechanisms that are incentive compatible, individually rational and guarantee budget balance.
• If the cost of funding the public good is small in comparison to the total size of the economy and the number of people interested in the public good, then the average cost will approach zero. This allows us to get arbitrarily close to giving everyone access to the public good. See also this paper by Martin Hellwig.

Regarding the history of the fixed fee mechanism with average cost prices, I want to mention that average cost prices have been studied for a very long time in the context of monopoly economics and a number of authors have examined fixed fee mechanisms in the context of public goods. However, as far as I was able to find out, the paper by Peter Norman is the first instance where this exact mechanism has been studied in a public good setting.

Of course there is a lot more to say about these results and I plan to write more about the technical details in the future. But today, I want to talk about how this mechanism could work in practice and present a practical implementation which I dub the Average Cost Threshold Protocol.

The Average Cost Threshold Protocol in Practice

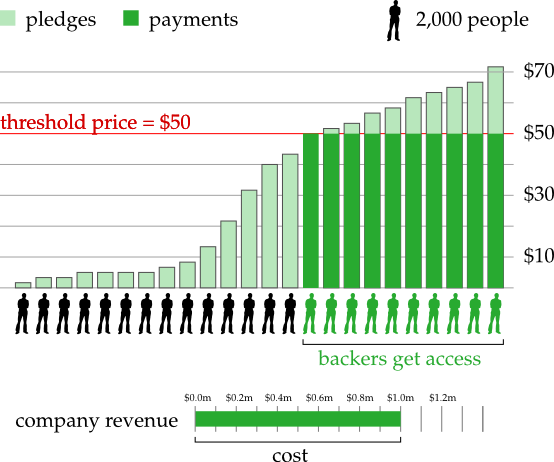
Suppose a company wants to create a computer game and they need money to cover their costs, which total, say, $1 million. They decide to use the above mechanism to raise the funds and so they start a project on a website like Kickstarter which provides all the necessary infrastructure. The project is open to receive pledges for 30 days and at the end of that period the pledges are tallied to see if the project can be funded according to the above rule. (Strictly speaking, setting a deadline is not necessary, but given that many crowd-funding projects raise a large part of their funds the days immediately before the deadline, it seems like a good idea to make use of this psychological effect.)

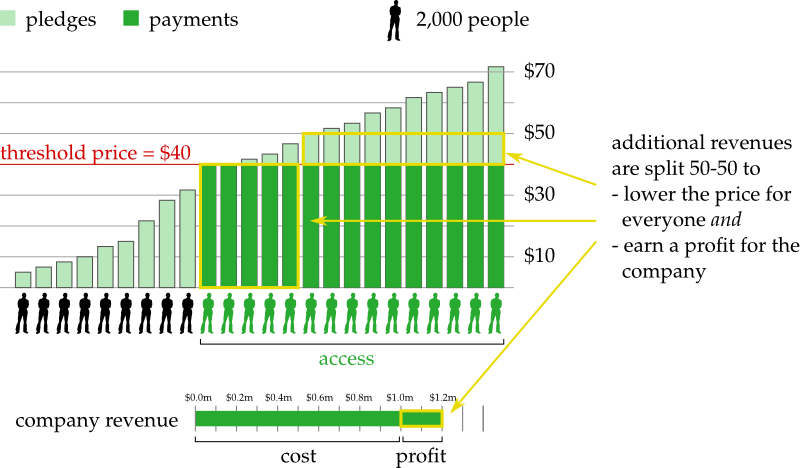
Many people chip in and pledge various amounts. There are 20,000 people who pledge \$50 or more. So setting a price of \$50 would exactly cover the costs of the game. However, there are only 23,000 people who pledge \$40 or more, so setting a price of \$40 would raise only \$0.92 million which does not cover the costs of the game. Let us assume that \$50 is the lowest price that covers the costs of the game.

Thus, the price is fixed at \$50 dollars. Everybody who pledged \$50 or more now has to pay exactly \$50 dollars. The people who pay these \$50 are now called backers. The total amount raised is \$1 million which covers the costs of the game. This money is used to create the game, and once it is finished, every backer receives a copy.

So far so good. But what about all the other people who would like to play the game? In all likelihood, there are many more people out there who would be happy to pay \$50 to get a copy! Maybe they heard about the project only after the fundraising ended, so they did not have a chance to become a backer. Or maybe they wanted to wait and see how the game turned out before committing to the purchase. Or maybe they did not have \$50 to spare back then, but they do now. Whatever their reasons, it makes perfect sense to provide these people with the public good - we just have to find a way that is consistent with our mechanism.

How do games companies currently do it on Kickstarter? Well, they just sell copies of the game. And the companies keep the revenues from these sales for their own profit. There is nothing wrong with creators making a profit from their work. The problem here is that this breaks our mechanism! Suppose there are another 20,000 people (let's call them buyers as opposed to backers) who pay \$50 for the game and these revenues are the profits of the company. Now there are a total of 40,000 people (buyers + backers) who have paid \$50 each, which amounts to a total of \$2 million dollars. However distributing the total cost of the game (\$1 million) among 40,000 people would lead to an average cost of just \$25! So, in this scenario, if the company decides to sell the game for profit after it is finished, people would pay twice the average cost, which is very different from what our mechanism specifies.

So let's suppose we take our mechanism seriously. What would need to happen with the profits from selling the game? Suppose we have 20,000 backers plus 20,000 buyers. As we observed above, distributing the costs of \$1 million equally among those 40,000 people would lead to an average cost of just \$25. But the backers already paid \$50! So here is what needs to happen according to the mechanism: The buyers need to pay just \$25 each. And these revenues need to be given to the backers instead of the company. This makes sure that everybody pays exactly the average cost of the public good.

But now the price of the good has dropped by 50% and the product is gaining ever more public attention. So now there are, say, 40,000 additional people out there who would be willing to pay \$25 for the game. Here is what the mechanism tells us to do: Charge each of the 40,000 newcomers \$12.50 and give the proceeds to the 40,000 people who purchased the game first. This way, everybody just paid \$12.50.

You can now see where this is going:

• As more and more people buy the public good, the average cost of the good drops.
• The price of the good drops, making the good available to more and more people.
• In this process, early buyers are refunded for the high price they paid in the beginning.
• In particular, because of the transfers from late buyers to early buyers, nobody has an incentive to wait with their purchase until prices drop.

All we need for this to work is for the website that coordinates this process to manage these transfer payments. Of course actually distributing money among many different bank accounts whenever a single purchase is made would incur way too much transaction costs. But the website could simply keep track of purchases and how revenue needs to be redistributed and allow customers to withdraw funds every once in a while. The transaction costs could be passed on to backers/buyers directly or could they could simply be financed from the interest the website earns from keeping the payments for some time.

It is also important to note that the infrastructure for pledging available on the website should still be used for sales, even after the product is finished. This way, if the current price for the game is still \$40, people who would be willing to pay \$20 for the product could submit this "bid" on the website. If enough people pledge \$20, the price of the product will actually drop and they will get a copy. The important thing is that people have an incentive to reveal the true price they are willing to pay! This is in contrast to a classical sales context, where customers have an incentive to understate their true valuation to get the company to lower their price.

The Benefits in Summary

The Average Cost Threshold Protocol is a practical mechanism for funding public goods that allow use exclusions. It is an implementation of the well-known fixed fee mechanism with average cost prices, and thus it enjoys many desirable properties:

• It is in everybody's own best interest to pledge exactly what they are willing to pay. This is true even in hindsight!
• The protocol makes everybody better off. In particular, nobody is forced to pay anything.
• The costs of the project are guaranteed to be covered for the company.
• Among all possible mechanisms with these properties this one is optimal, that is, it creates the most value for society as a whole.

Beyond these theoretical merits, the practical protocol suggested above has a number of additional benefits:

• Prices to the public good are lowered continuously, in order to provide the widest possible audience with access to the public good as quickly as possible.
• At all times throughout the process, everybody has paid exactly the same price for access to the public good. So nobody has an incentive to wait with their purchase for prices to drop.
• In the sales-phase, it is in the interest of customers to bid what they would be willing to pay, even before prices drop. This allows the mechanism to lower prices more quickly, via optimal price targeting.
• Everybody benefits from getting more people to buy access. Even today, backers of crowd-funding projects often provide significant marketing services to their projects through word of mouth, long after fundraising has ended. Using this protocol, backers are not only personally rewarded for this engagement, but they also help to give more people access at lower prices.

Of course this is not the end of the story! There are a number of variants of this mechanism that are worth exploring.

Variations of the Protocol

There are a number of aspects of the basic version of the Average Cost Threshold Protocol presented above which can be improved further.

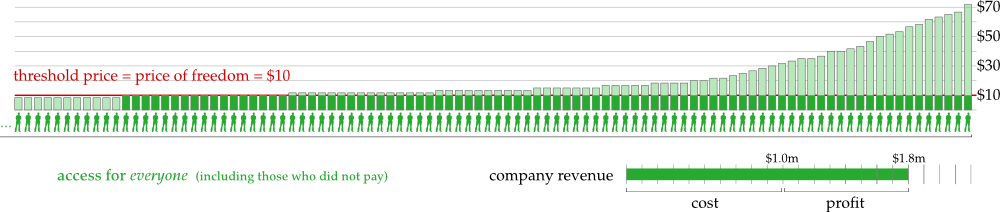
1) Most importantly, the public good provided by the protocol is still subject to use exclusions. We would really like to actually provide a pure public good that everybody has access to, no matter if they paid anything or not. But if we modified the mechanism so that people know the good is eventually going to be provided for free, the economic incentive to contribute something would disappear. Remember, this is the essence of the Myerson-Satterthwaite impossibility theorem!

Nonetheless, there are a number of ways the protocol could be modified to fund the creation of a pure public good without use exclusions. For example, we could set a "reserve price" of, say, \$5 dollars. If the price of the good falls below \$5, the good becomes a pure public good available to everyone for free. Now, of course, everyone who did pay \$5 has paid \$5 too much, which would destroy incentive compatibility in a strict sense. But as \$5 is a relatively small loss, backers who care about the project may very well be ready to accept this loss and gain the warm glow-effect of having made the public good available for everyone. Instead of fixing a common reserve price of \$5 for everyone, backers might also set their own individual reserve price when buying the product. (This of course would require the redistribution scheme to be adjusted.)

A completely different option would be to set a fixed "expiration date" of the use exclusions, for example, three years after the release of the finished product. Buyers would then purchase early access to the product, which is a common business model already today. The difference is that this early access would come with a guarantee that the product will become a pure public good eventually.

Of course such modifications would ruin some of the nice game theoretical properties of the mechanism. But these theorems hinge on the assumption that all backers are entirely rational anyway. And humans are not entirely rational, they are also benevolent and they tend to be tremendously enthusiastic about creative projects they like. So there is room enough for such small changes to work, even if they don't fit into the rational framework.

2) Companies or creative individuals funding a project using the "vanilla" Average Cost Threshold Protocol as defined above enjoy the tremendous benefit of having their costs covered in advance by payments very similar to pre-purchases. They are not funded through equity and they have no liabilities, which means they have no investors that they need to satisfy through profits and they have no debt that they need to pay off. But that does not mean that all is well.

First of all, after the project is funded and the company received the payment to cover their costs, they are not going to receive any further payments, whatsoever. This means that they have no further economic incentives to make the project succeed. They may have incentives in terms of their creative ambition, their reputation as a company, their individual careers or simply their personal integrity. But the economic incentives to make the product shine, to market it well, to finish it on time and on budget or even to complete the project all - they are all gone. This is clearly not in the interest of anybody! Therefore it is a good idea to allow the company to make some profits in order to create the corresponding economic incentives.

Moreover, no matter how accurately the company projected the costs of the project at the outset, the actual development may run over budget. Projects often (always?) do. So despite the fact that the initial fundraising is expected to cover costs in advance, the company still faces financial risks. To make these financial risks worthwhile to the company, it stands to reason that the company is allowed to make some profit.

Fortunately it is straightforward to allow the company to make a profit and at the same time allow the public to enjoy decreasing prices. The rule is simple: Half of the payment a new buyer makes goes to the previous backers, the other half is profit for the company. An example. Initially, 20,000 backers paid \$50 each to raise \$1 million. Now, 10,000 additional buyers want access. According to the original protocol, everybody would have to pay \$33.33 now. But instead, we ask the newcomers to pay \$40. Half of that is the profit of the company, which amounts to \$200,000 in total. The other half goes towards refunding the original 20,000 backers so that everybody paid just \$40 in total. In this way, prices will decrease steadily with an increasing number of buyers. But still, the company stands to make an unlimited profit from creating a great product! This amounts to a reasonable compromise between the interests of the company and the social goal of giving access to as many people as possible.

The great thing about this variation is that it preserves many of the nice game-theoretic properties of the original mechanism. In particular, this modified mechanism is still incentive compatible and individually rational. It still covers costs by producing a budget surplus instead of a balanced budget. It is less efficient than before, because fewer people get access for the same amount of money. But still, as the number of buyers grows, the price goes to zero, enabling everybody to afford access if the public good becomes popular enough.

Of course, nobody says that revenues always have to be split 50-50 among the company and its backers. Any other ratio would do. The ratio could change over time. Or each backer could choose their own ratio (similar to what the Humble Bundle is doing), leading to a democratic vote on how revenues should be split. Also, this idea can be combined with the first variation presented above to create a protocol that produces both profits for the company and a public good without use exclusions, provided the good becomes popular enough. In this case the profits for the company are bounded and it is not entirely rational for buyers to reveal their true valuation, but still this promises to be an excellent compromise.

3) From a game theoretic perspective it is important (though not indispensable) that everybody pays the same price. However, from a practical perspective that may not be desirable. Some backers may want to be charged more than other backers. Maybe because they want to show how much they value the project. Maybe the company decides to offer rewards for backers who pay much. Most importantly, there is a real possibility that projects cannot be funded without backers who self-select to pay a very large premium on the average cost. The public interest in the project may not be broad enough to get the costs covered on an average cost pricing basis, but the interest may well be deep enough to cover costs if some people are allowed to pay more.

A special case is the money the company itself puts into the development. Companies and creators running crowd-funding projects often put a significant amount of personal wealth into their projects. Usually, these are funds that do not show up during the fundraising campaign. But an effective mechanism for funding public goods should explicitly incorporate a facility to account for this common practice.

Again there are several ways to allow backers to pay more than the average cost during the initial fundraising campaign. (Note that backers can always pledge as much as they want, but in the original protocol, they will never pay more than the average cost.) One way to accommodate this is via the variable reserve price mechanism mentioned above. Backers who want to pay a lot could simply set their personal reserve price to exactly the same amount as their pledge. Then, they could get charged the entire amount if the fundraising campaign is successful.

However, the above variation would also imply that these backers are not refunded anything. This may well be in the interest of very enthusiastic backers, but it would not fit the needs of the company who wants to recoup the large investment it made into the project in this way. Also there may be backers who are willing to make a very large payment, if the project can't be funded otherwise, but would like to be refunded if the project turns out to be widely popular in the long run. To accommodate these interests, one could allow backers to specify that they want to be charged more during the fundraising campaign. Later on, the revenues earned from sales of the product could be used to refund backers in proportion to the payment they made during fundraising. This way large backers could eventually recoup their investment if the project is widely successful.

While it may generally not be rational for backers to make such large payments, the presence of this option does not change the fact that for the average backer the protocol remains incentive compatible and individually rational. As before, this variation can also be combined with the variations 1) and 2) mentioned above.

Conclusion

The Average Cost Threshold Protocol and its variations promise to yield an effective mechanism for the private funding of public goods. Even if this particular mechanism is not the ultimate answer, it shows that there is a lot of room out there for improving upon existing crowd-funding mechanisms in this regard. I hope that more people apply their creativity to invent new ways of making the private provision of public goods attractive. In a world where public goods make up an increasing share of the global economic output, such a mechanism could change the way we do business and interact with each other's creative work.

This paper is a continuation of the work that Matthias Beck and Thomas Zaslavsky started on using inside-out polytopes to prove reciprocity results for counting polynomials and that Raman Sanyal and I adapted to the case of modular counting functions. In the present work we generalize all of this considerably, by proving a whole collection of combinatorial reciprocity theorems for flow, tension and chromatic quasipolynomials defined on cell complexes, i.e., in terms of arbitrary integer matrices. The fact that the Ehrhart theory methods developed for the graph case do generalize to cell complexes is a testament to the remarkable power of the geometric approach to combinatorics. Head over here to hear the full story!

Crowd funding really took off in 2012. From my personal perspective, the most visible embodiment of this trend was the emergence of Kickstarter as a means of funding game development projects. Double Fine Adventure was one of the first projects that brought this concept to public attention by raising $3.3 million. This was quickly followed by the success of such projects as The Banner Saga ($723k), Shadowrun Returns ($1.8m), Star Citizen ($2.1m) and Project Eternity ($4.0m). Of all of these, I think The Banner Saga stands out, as it is a very original project by a comparatively unknown team, whereas the other projects capitalized on well-established concepts and the fame of their celebrity project-leaders.

When I first encountered Kickstarter, I became very excited, not just because of the addictive warm-glow effect of making great projects happen, but also because Kickstarter struck me as the first large-scale, widely popular implementation of the Street Performer Protocol. The Street Performer Protocol is a brand name coined in the 90s by Steven Schear, John Kelsey and Bruce Schneier for a very simple and very old mechanism for fundraising: Artists announce that they will do a public performance if the audience as a whole pays a fixed total amount (or more). If enough spectators chip in to reach this threshold, the artists collect the money and perform. Otherwise, nobody pays anything and there is no performance. This is essentially how Kickstarter operates.

Now, back in the 90s, the Street Performer Protocol (SPP) was heralded as a mechanism for funding public goods. A public good is a good that, once it is created, can be enjoyed by anybody without being "used up". (See the end of this post for more details on the term.) Software and computer games make excellent examples of public goods in that they can be copied perfectly at a vanishingly small cost.

Commercial publishers of software and games often impose legal and technical restrictions on copying. They create use-exclusions in order to be able to sell the software like a classical private good. While this is a perfectly valid business model, it seems wasteful because it prevents people from using the software who could benefit from it at no additional cost. By contrast, the open source / free software model of software development ensures that free copying is possible, both legally and technically. But if software is to be made available as a public good without use-exclusions, how is its development to be funded? People hoped the SPP might provide an answer to this question, and, sure enough, the SPP soon had important successes. For example, in 2002, Ton Roosendaal managed to raise €100,000 in order to buy the rights to the 3d software Blender (that he created) from the creditors of his bankrupt company NaN and released Blender under the GPL. But despite such isolated successes the SPP did not gain widespread adoption, and cross-subsidies remained/became the primary source of funding for open source software projects.

With all of this in mind, I became very excited when I discovered how successful Kickstarter was. Did we finally have a working way of financing the private provision of public goods directly? My enthusiasm led me to contribute funds to a couple of projects on Kickstarter, which has been a great experience all around. But. This experience also made it clear that, contrary to my first hopes, Kickstarter is not about the provision of public goods and it is not used to implement the SPP - at least judging by the way it is used in the game development community.

None of the games mentioned above are going to be released as a public good when they are completed. Instead, they are going to be sold, with the profit to be shared by the development studio, possible publishers and whatever investors they may have. The Kickstarter backers are not investors in this context. Their pledge is not a contribution towards the creation of a public good, it just buys a single license for a future product and is thus seen as, merely, a pre-order. From this point of view, customers buy a product years in advance that they know virtually nothing about. Moreover they self-select for price targeting by voluntarily paying much more than price of the pre-order. (This price targeting is significant. All aforementioned projects had individual backers pledging more than $10,000 dollars and a significant percentage of backers pledged more than double the price of the respective pre-order.) In exchange for these additional funds, they get additional merchandise of limited value and the warm-glow effect of being part of a project they care about.

To be sure, this long-term pre-order model of funding games does potentially have great positive effects. When an audience not only buys the product but funds the creation process from the start, stakeholders become the key financiers of the project, which may lead to fewer conflicts of interest. Development teams achieve greater creative independence, they can follow their instincts and have to worry less about mass market appeal and investor interests. In the most optimistic scenario, this can lead to a more satisfying experience, both for the developers and for the customers.

Nonetheless, treating a Kickstarter pledge as a "pre-order" sounds just wrong to me, for several reasons. First of all, backers take on a large amount of risk with their pledge. They have no guarantees that the product is going to be delivered, they have no influence on the creation process, they have no information about the product they are buying, the price they pay is, on average, way above the final market price of the product, and they receive none of the revenues made by selling the final product. In short, if Kickstarter is used to create software that is going to be sold for-profit, then backers make a huge investment, reap none of the profits that arise from their investment, carry a large share of the risk, and end up paying much more than customers who buy the product after it has been released.

To be clear: I do think that all of the aforementioned projects are run by development studios with the best intentions. And while contributing on Kickstarter does have a warm-glow effect that can be addictive, I am convinced that most backers are rational in their decision. The huge transfer payment from backers to developers inherent in the pre-order funding model described above is a deliberate decision to fund art that would not be created without such a payment. But for studios to dismiss this huge gift as a pre-order and then to sell the resulting product exclusively for their own profit strikes a wrong chord with me.

Now, the pre-order model is certainly not the only way Kickstarter is used. The are projects, such as Chris Granger's wonderful Light Table project, that were created with the explicit purpose of producing open source software. The Light Table Kickstarter project raised $316,720 and makes a prime example of the use of the Street Performer Protocol for funding a public good. I do hope that other Kickstarter projects will have the courage to ask backers for money, even if they pledge to make their final product open source upon release. In my view, this would be a much fairer deal. Projects such as LightTable (and Blender ten years ago) show that this can work, despite the fact that it is not rational in a strict economic sense for an individual backer to donate money to such a development project. If this mode of using Kickstarter catches on, we will have a truly new way of financing public goods. Such a mechanism would have a huge impact, given that an ever-growing share of the global economy deals in virtual goods that could in principle be turned into public goods.

So, I do still have hopes for more public good projects on Kickstarter. But hope is not good enough!

Therefore, I will use this post to kick off a series of posts on the economics of public goods, dealing with questions such as: What other mechanisms for funding public goods are out there? What tools do we need to analyse such mechanisms? What are the theoretical limits? How would a funding platform for the private provision of public goods have to work in order to be widely successful?

Addendum: One paragraph introduction to public goods. A public good is a good that, once it is created, can be enjoyed by anybody without being "used up". Anyone can stand by and watch a street performance, once it is happening. Anyone can walk on a street, once it is built. And anyone can make a copy of a digital movie, once it has been created, without anyone having "less" of the movie. Of course this is not quite true. A performance may become too crowded for new arrivals to see anything, and a street may become too congested for anybody to walk or drive. So, under extreme conditions there is some rivalry in the consumption of these good, but in most cases one more onlooker or one more pedestrian does not "cost" anything, which makes these goods non-rival. Now, as far as digital movies are concerned, their copying is perfectly non-rival as both copies are identical and nobody has "less" of the movie. However, there are often many legal and technological barriers in place to prevent consumers from copying. That is, the industry tries (with moderate success) to exclude consumers from obtaining a copy the movie, if they did not pay for it. When these restrictions are not in place, there is nothing preventing a consumer from making a copy, and the movie becomes a public good without use-exclusions. A pure public good is perfectly non-rival and non-excludable. In practice, public goods often have some limited rivalry, but it may still be instructive to think about them as public goods as they are non-rival in most cases. For my purposes, I do not include non-excludability in my definition of a public good, as the role of use-exclusions in the funding of public goods is precisely what I want to discuss.