It has been up on the arXiv since the beginning of April, but only now do I get to announcing it here: Martina Kubitzke, Aaron Dall and myself published our article on Hypergraph Coloring Complexes. Here is the abstract:
The aim of this paper is to generalize the notion of the coloring complex of a graph to hypergraphs. We present three different interpretations of those complexes – a purely combinatorial one and two geometric ones. It is shown, that most of the properties, which are known to be true for coloring complexes of graphs, break down in this more general setting, e.g., Cohen-Macaulayness and partitionabilty. Nevertheless, we are able to provide bounds for the $f$- and $h$-vectors of those complexes which yield new bounds on chromatic polynomials of hypergraphs. Moreover, it is shown that the coloring complex of a hypergraph has a wedge decomposition, though we conjecture that in general this decomposition is not homotopy equivalent to a wedge of spheres. In addition, we can completely characterize those hypergraphs whose coloring complex is connected.
You can find the complete article on the arXiv.
A Conjecture
For those of you who like a challenge, I want to highlight an open problem, that we present in the article. We conjecture that in general, hypergraph coloring complexes do not have the homotopy type of a one-point wedge of spheres.
Actually, this statement is true by virtue of the fact that there are hypergraphs that have disconnected coloring complexes. So the conjecture really is that even among the connected hypergraph coloring complexes, there are some that are not wedges of spheres.
As it turns out, we even have a candidate for a counterexample, i.e., a hypergraph coloring complex that we think is not a wedge of spheres. However, we have not been able to prove that yet.
Our candidate hypergraph $G$ is a graph on vertex set $V=\{1,\ldots,9\}$ with edge set
\[
E=\{12347,12358,12369,14567,24568,34569,14789,25789,36789\}.
\]
If you arrange the vertices in a 3×3 grid, the edges can be represented visually like this:

What is the idea behind this? Every edge in the hypergraph corresponds to a sphere in the coloring complex, which we call edge spheres and denote by, e.g., $P_{12347}$. The idea is to build up a torus out of edge spheres like this:
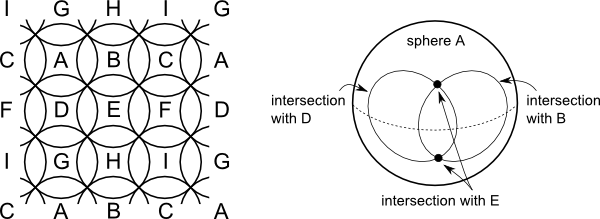
All edge spheres in this example are 3-dimensional. Any two edge spheres that are horizontally or vertically adjacent, for example $P_{12358}$ and $P_{24568}$, intersect in a 1-dimensional sphere. Any two edge spheres that are diagonally adjacent, for example $P_{12347}$ and $P_{24568}$, intersect in a 0-dimensional sphere. However, any three edge spheres meet all three columns or all three rows in the above 3×3 grid have an empty intersection. This suggests that the coloring complex $\Delta_G$ does indeed have the structure we are aiming at.
All that remains is to check if this complex does have the homotopy type of a wedge of spheres. One tool to use for this is to compute the multiplicative structure of cohomology ring of of this complex, i.e., to compute cup products. In principle, this is straightforward. In practice, however, even computing the cohomology of this complex will require wrangling coboundary maps whose matrices have hundreds of columns. This you do not want to do by hand! However all the algebra software we looked at, including GAP and Sage, is not able to compute cup products. A facility to compute cohomology rings of simplicial complexes is planned to be added in a future version of Sage. Until then, our efforts to settle this conjecture rest.
But maybe you know how to compute this with current technology (or maybe even pen and paper)?
Update: Using Sage we have answered our conjecture positively: The coloring complex of the graph defined above is not a wedge of spheres. See the latest version of our paper on the arXiv.