In the last post I elaborated on the overall design of InkBoard, my pen-centric on-screen keyboard. In this post, I want to write about the design of the default layout of InkBoard, i.e. where the individual characters are placed on the radial menu. Note that I am only interested in the primary layer of the layout here. The secondary layer with additional characters, including numbers, I will not talk about, as I did not invest much thought into its layout. There are quite a few things to say about the primary layer, however.

Theory

The primary layer of the default layout looks like this:

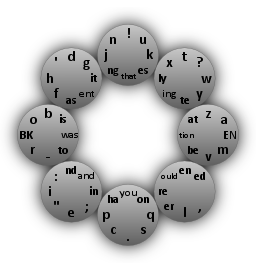
This picture can be read as follows. Let us denote the eight menu items with compass directions, such that, e.g., NE stands for the top-left menu item. Then, e.g., the letter ‘a’ can be typed by selecting the menu items E-NE in that order. The character sequence ‘tion’ can be typed by selecting E-W and the character sequence ’the ’, including a trailing space, can be typed via NE-N-NW-W-SW-S-SE-E.

The goal is to produce a layout that allows English plain text to be written efficiently.

To optimize a layout with regard to the attainable writing speed, you need to know which combinations of menu items are easy to select using strokes. I have no empirical data about this (yet), so I needed to make an educated guess. The one assumption this layout is built upon is this:

It is easiest to select adjacent menu items with a stroke.

So S-SW is easier to type than S-W and NW-N is easier to type than NW-E or NW-SE. There are 16 ordered pairs of adjacent menu items: There are 8 possible starting items and each item has 2 items adjacent to it. These 16 pairs correspond to the following positions in the layout:

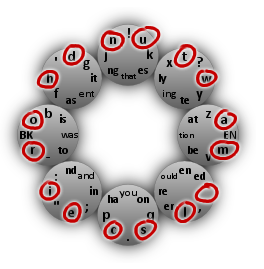
The assumption now dictates that these 16 positions should hold the 16 most commonly used characters in plain in English text. According to Wikipedia these are the space and the letters

e t a o i n s h r d l c u m w

and, sure enough, these are precisely the characters I chose for these 16 positions. The important questions, though, is:

p(indent). How should these 16 characters be arranged?

Going by the above assumption, characters that frequently follow each other should be placed next to each other. For example, if the most frequent character to occur after an ‘a’ in English plain text is ‘n’, and ‘a’ can be typed by selecting E-NE, then ‘n’ should correspond to N-NW.

Given that ‘a’ is on E-NE, another option would be to place ‘n’ on E-SE. But here another assumption of mine entered:

Reversing the direction of the stroke is ‘expensive’.

E-NE requires a stroke in clockwise direction. N-NW is clockwise as well, whereas E-SE is counter-clockwise. Thus N-NW is the best position for ‘n’ given that ‘a’ is on E-NE.

Gathering data

To be able to apply these theoretical observations, however, I needed data.

For each of the 16 most common characters, what is the character that is most likely to follow?

Wikipedia was no help here and Google did not turn up anything either, so I had to make my own experiments. Fortunately, Project Gutenberg makes many works of English fiction freely available as plain text. I picked three at random, namely

1. “Pride and Prejudice” by Jane Austen
2. “David Copperfield” by Charles Dickens
3. “Hamlet” by William Shakespeare

and wrote some Clojure code. First we simply read in the texts.

(def austen "c:/Users/Felix/.../austen.txt")
(def dickens "c:/Users/Felix/.../dickens.txt")
(def shakespeare "c:/Users/Felix/.../shakespeare.txt")

(def austen-str (slurp austen))
(def dickens-str (slurp dickens))
(def shakespeare-str (slurp shakespeare))
(def all-str (concat austen-str dickens-str shakespeare-str))

Given a text and a size we consider all substrings of length size of the text. As we iterate over these substrings, we construct a map that associates each substring with the number of appearances of the substring in the text. The map we keep in a reference called statistics.

(defn update-stats [substring statistics]
  (dosync
   (ref-set statistics
            (let [stats @statistics]
              (if (nil? (stats substring))
                (assoc stats substring 1)
                (update-in stats [substring] inc))))))

(defn count-substrings [text size statistics]
  (let [theseq (if (= size 1)
                 text
                 (partition size (dec size) text))] 
    (doseq [substring theseq]
      (update-stats substring statistics))))

After we have used these functions to gather the data, all we need to do is to order the substrings by the number of occurrences and print the result.

(defn sorted-stats [statistics]
  (let [stats @statistics
        substrings (keys stats)
        sorted (sort-by stats substrings)
        result (take 120 (reverse sorted))]
    (doseq [substring result]
      (println substring (stats substring)))))

(defn analyze [text size]
  (let [statistics (ref {})]
    (count-substrings text size statistics)
    (sorted-stats statistics)))

Now, what statistics do we get from the texts? Let us start with simple character counts and see if we can confirm the statistics from Wikipedia.

user> (analyze dickens-str 1)
  328544
e 179484
t 129004
a 119416
o 114683
n 101316
i 92897
h 88134
s 87890
r 85729
d 67836
l 55819
u 41924
m 40218
\n 38587
^M 38586
w 36615
, 36367
y 32741
c 32176
f 32090
g 30926
p 24148
b 21429
' 19841
. 18525
I 15394
v 13701
k 13319
</pre>

We note that the space is by far the most frequent character. The \n and ^M both correspond to the newline, which is among the top 16 characters. This, however, is due to the fact that Project Gutenberg do not rely on automatic line wrapping; instead each paragraph is broken into lines explicitly. So we will ignore these entries. The next thing to note is that the comma is among the top 16, but I chose to ignore that one as well. Also, I did not lowercase the texts before doing the analysis. The most frequent capital letter is ‘I’, outside the top 20. The final observation is that, as far as the letters are concerned, the ‘y’ is among the top 15 letters instead of the ‘c’.

Repeating the same experiment with the other two texts yields similar results. In Austen’s novel both the ‘c’ and ‘y’ are among the top 15 at the expense of ‘w’ and in Shakespeare’s play, again, ‘y’ and ‘w’ are among the top 15 at the expense of ‘c’. On the whole, this suggests modifying the Wikipedia ranking to include ‘y’ instead of ‘c’ in the top 15, but I did not take that step.

Let us now move on to substrings of size 2. The first few entries look like this. (I already removed the newline.)

user> (analyze dickens-str 2)
(e  ) 48306
(  t) 40457
(  a) 37122
(h e) 36084
(t h) 35559
(d  ) 35168
(,  ) 31493
(t  ) 29790
(i n) 27645
(e r) 26733
(s  ) 24650
(  h) 23246
(  w) 22941
(a n) 22865
(  s) 22734
(n  ) 19706
(r e) 19210
(n d) 18962
(  o) 18273
(h a) 17762
(y  ) 17343
(  m) 17103
(o u) 16884
(r  ) 16006
(  i) 15808
(a t) 15754
(o n) 15486
(t o) 14967
(o  ) 14837
(e d) 14713
(e n) 14208
(n g) 13962
(i t) 13361
(  b) 13113
(a s) 12751
(.  ) 12111
(o r) 12109

As we can see, most of the most frequent two-character substrings involve a space. Most importantly, ‘e’ should be adjacent to the space. Common two-letter substrings are ‘he’, ‘th’, ‘in’, ‘er’, ‘an’, ‘re’ and ‘nd’. Again, the situation with the other two works is similar.

From data to layout

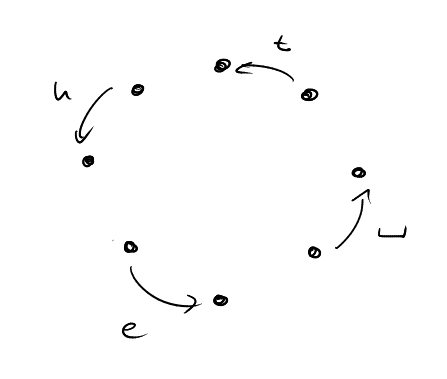
The first few lines in the above table make it clear that space should be followed by ‘t’, ‘t’ should be followed by ‘h’, ‘h’ should be followed by ‘e’ and ‘e’ should be followed by space. This already gives the following rough structure of a layout. (Here the arrow labled ‘t’, for example, denotes the selection sequence NE-N.)

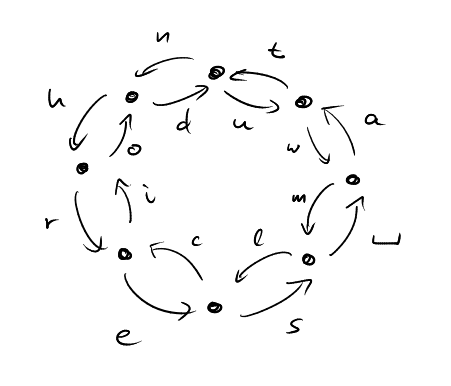
Looking further at this table we see that ‘a’ should be followed by ‘n’ and close to ‘t’, ‘r’ should be close to ‘e’, ‘o’ should be followed by ‘u’ and close to ‘n’ and ‘t’. By continuing in this fashion, I came up with the following layout of the 16 primary positions.

I then went on to fill in the remaining positions. Here I proceeded in a much more ad-hoc way. On the assumption that “90-degree turns” such as N-E or NW-SW are not too difficult, I placed all the remaining letters there. On the assumption that selecting the same entry twice in succession feels a bit awkward, I used these positions for the punctuation marks, also because these moves are easy to memorize.

This still left quite a few positions open. I decided to try and fill these with common character sequences. The inspiration here were classical shorthand systems that, for example, have special symbols for common suffixes like ‘tion’ or ‘ing’. So I had a look at the most common substrings of sizes 3, 4 and 5. Of these I selected a few that I felt could not be written easily enough with the layout as it stood thus far, including ‘you’, ‘and’, ‘ing’, ‘that’, ‘tion’ and ‘ould’. The most frequent sequence of 3 letters in all three texts is ‘the’. However as ‘the’ is particularly easy to write with the primary layout, I did not add ‘the’ as a character sequence. On the whole, the choice of the character sequences and their position on the layout does feel somewhat arbitrary to me. There is a lot of room for improvement here.

The next step

The next step is to formulate the layout design problem as a formal optimization problem and use, say, linear programming to find an optimal solution. The major obstacle on this path is to quantify the cost of all possible movements. How much more “difficult” is N-NE-E-NE than N-NE-E-SE? Is N-E truly easier than N-SE, or is it the other way around? Other common sequences on the current layout involve touching menu items twice (e.g., ‘res’ W-SW-SW-S-S-SE), crossing the entire inkboard (e.g., ‘ha’ NW-W-E-NE) or making reversals (e.g., ‘in’ SW-W-N-NW). What are their relative costs? Moreover, does the position of the sequence on the InkBoard matter? For example, is SE-E easier to write than SW-S?

A formal model of “difficulty” or “cost” is required. This should take at least two factors into account.

1. The time it takes a trained user to write the given sequence.
2. The error rate of a trained user when writing the given sequence.

After a cost has been defined, empirical measurements are in order to determine the actual cost of all the sequences. Ideally such measurements would be made automatically by a training program. Developing such a training program is the next big item on InkBoard’s to-do list.